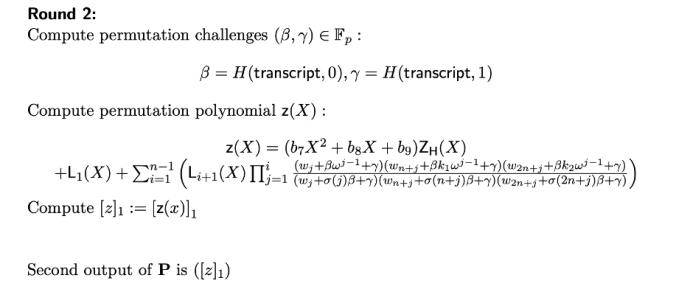By Jim Miller
In part 1 of this blog post, we disclosed critical vulnerabilities that break the soundness of multiple implementations of zero-knowledge proof systems. This class of vulnerability, which we dubbed Frozen Heart, is caused by insecure implementations of the Fiat-Shamir transformation that allow malicious users to forge proofs for random statements. In part 2 and part 3 of the blog post, we demonstrated how to exploit a Frozen Heart vulnerability in two specific proof systems: Girault’s proof of knowledge and Bulletproofs. In this part, we will look at the Frozen Heart vulnerability in PlonK.
Zero-Knowledge Proofs and the Fiat-Shamir Transformation
This post assumes that you possess some familiarity with zero-knowledge proofs. If you would like to read more about them, there are several helpful blog posts and videos available to you, such as Matt Green’s primer. To learn more about the Fiat-Shamir transformation, check out the blog post I wrote explaining it in more detail. You can also check out ZKDocs for more information about both topics.
PlonK
The PlonK proof system is one of the latest ZK-SNARK schemes to be developed in the last few years. SNARKs are essentially a specialized group of zero-knowledge proof systems that have very efficient proof size and verification costs. For more information on SNARKs, I highly recommend reading Zcash’s blog series.
Most SNARKs require a trusted setup ceremony. In this ceremony, a group of parties generates a set of values that are structured in a particular way. Importantly, nobody in this group can know the underlying secrets for this set of values (otherwise the proof system can be broken). This ceremony is not ideal, as users of these proof systems have to trust that some group generates these values honestly and securely, otherwise the entire proof system is insecure.
Older SNARK systems need to perform this ceremony multiple times for each program. PlonK’s universal and updateable trusted setup is much nicer; only one trusted setup ceremony is required to prove statements for multiple programs.
In the next section, I will walk through the full PlonK protocol to demonstrate how a Frozen Heart vulnerability works. However, PlonK is quite complex, so this section may be difficult to follow. If you’d like to learn more about how PlonK works, I highly recommend reading Vitalik Buterin’s blog post and watching David Wong’s YouTube series.
The Frozen Heart Vulnerability in PlonK
As in Bulletproofs, PlonK contains multiple Fiat-Shamir transformations. Each of these transformations, if implemented incorrectly, could contain a Frozen Heart vulnerability. I will focus on one particular vulnerability that appears to be the most common. This is the vulnerability that affected Dusk Network’s plonk, Iden3’s SnarkJS, and ConsenSys’ gnark.
PlonK, like most SNARKs, is used to prove that a certain computation was performed correctly. In a process called arithmetization, the computation is represented in a format that the proof system can interpret: polynomials and arithmetic circuits.
We can think of the inputs to the computation as input wires in a circuit. For SNARKs, there are public and private inputs. The private inputs are wires in the circuit that only the prover sees. The public inputs are the remaining wires, seen by both the prover and the verifier.
Other public values include the values generated by the trusted setup ceremony used to generate and verify proofs. Additionally, because the prover and verifier need to agree on the computation or program to be proven, a representation of the program’s circuit is shared publicly between both parties.
In part 1 of this series, we introduced a rule of thumb for securely implementing the Fiat-Shamir transformation: the Fiat-Shamir hash computation must include all public values from the zero-knowledge proof statement and all public values computed in the proof (i.e., all random “commitment” values). This means that the public inputs, the values from the trusted setup ceremony, the program’s circuit, and all the public values computed in the proof itself must be included in PlonK’s Fiat-Shamir transformations. The Frozen Heart vulnerability affecting the Dusk Network, Iden3, and ConsenSys codebases stems from their failure to include the public inputs in these computations. Let’s take a closer look.
Overview of the PlonK Protocol
PlonK has undergone a few revisions since it was first published, so a lot of the PlonK implementations are not based on the most recent version on the Cryptology ePrint archive. In this section, I will be focusing on this version posted in March 2020, as this (or a similar version) appears to be what the SnarkJS implementation is based on. Note: this vulnerability still applies to all versions of the paper, but for different versions, the exact details of how this issue can be exploited will differ.
Before diving into the details of the protocol, I will describe it at a high level. To produce a proof, the prover first constructs a series of commitments to various polynomials that represent the computation (specifically, they are constraints corresponding to the program’s circuit). After committing to these values, the prover constructs the opening proofs for these polynomials, which the verifier can verify using elliptic curve pairings. This polynomial committing and opening is done using the Kate polynomial commitment scheme. This scheme is complex, but it’s a core part of the PlonK protocol, and understanding it is key to understanding how PlonK works. Check out this blog post for more detail.
From the prover’s perspective, the protocol has five rounds in total, each of which computes a new Fiat-Shamir challenge. The following are all of the public and private inputs for the PlonK protocol:
Public and private inputs for the PlonK proof system (source)
The common preprocessed input contains the values from the trusted setup ceremony (the x[1]1, …, xn+2[1]1 values, where x[1]1 = g1x and g1 is the generator of an elliptic curve group) and the circuit representation of the program; these are shared by both the prover and verifier. The remaining values are the input wires to the program’s circuit. The public inputs are the public wires, and the prover’s input is both the public input and the prover’s private wires. With that established, we can start the first round of the protocol, in which the prover computes the blinded wire values.
Round 1 for the prover in the PlonK protocol (source)
The prover first computes three polynomials (a, b, and c) and then evaluates them at point x by using the values from the trusted setup ceremony. The underlying x value is not known (assuming the trusted setup ceremony was performed correctly), so the prover is producing a commitment to these polynomials without leaking any information. The prover does the same for the permutation polynomial in round 2:
Round 2 for the prover in the PlonK protocol (source)
We will not describe this round in detail, as it’s especially complex and irrelevant to this vulnerability. In summary, this round is responsible for enforcing the “copy constraints,” which ensure that the values assigned to all wires are consistent (i.e., it prevents a prover from assigning inconsistent values if one gate’s output is the input to another gate). From there, the prover computes the quotient polynomial in round 3. This quotient polynomial is crucial for the Frozen Heart vulnerability, as we will see shortly.
Round 3 for the prover in the PlonK protocol (source)
After round 3, the prover then computes the evaluation challenge, zeta, using the Fiat-Shamir technique. zeta is then used to evaluate all of the polynomials constructed up to this point. This zeta challenge value is the value we will target in the Frozen Heart vulnerability. As you can see, the authors of the paper use an ambiguous term, “transcript,” which they explain earlier in the paper to mean the preprocessed input, the public input, and the proof values generated along the way.
Round 4 for the prover in the PlonK protocol (source)
Finally, in round 5, the prover then generates the opening proof polynomials and returns the final proof.
Round 5 for the prover in the PlonK protocol (source)
To verify this proof, the verifier performs the following 12 steps:
At a high level, the verifier first verifies that the proof is well formed (steps 1-4), computes a series of values (steps 5-11), and then verifies them by using a single elliptic curve pairing operation (step 12). This check essentially verifies the divisibility of the constructed polynomials and will pass only if the polynomials are structured as expected (unless there’s a Frozen Heart vulnerability, of course).
Exploiting a Frozen Heart Vulnerability in PlonK
Recall that the Frozen Heart vulnerability in question stems from a failure to include the public inputs for the program’s circuit in any of the Fiat-Shamir challenge calculations (importantly, zeta). At a high level, a malicious prover can exploit this vulnerability by picking malicious public input values (that will depend on challenge values like zeta) to trick the verifier into reconstructing a t_bar in step 8 that will pass the final verification check. Let’s look at the details.
Recall that in round 1, the prover generates three polynomials (a, b, and c) based on the prover’s public and private wire values. If we are a malicious prover trying to forge proofs, then we don’t actually have these wire values (because we haven’t actually done any computation). Therefore, in round 1, we’ll generate completely random polynomials a’, b’, and c’ and then output their evaluations, [a’]1, [b’]1, and [c’]1.
Our random a, b, and c polynomials will break the polynomial computed in round 2 because this polynomial enforces the “copy constraints,” which means that wire values are consistent. With completely random polynomials, it’s essentially guaranteed that these constraints won’t hold. Fortunately, we can actually skip these checks entirely by zeroing out the round 2 polynomial and outputting [0]1. Note: if the implementation checks for the point at infinity, the verifier might reject this proof. If this is the case, you can be clever with how you generate a’, b’, and c’ so that the copy constraints hold, but the details of how that would work are a bit gnarly. Since the SnarkJS implementation does not return an error on this zeroed out polynomial, I will continue with this approach.
Now, for round 3, remember that we don’t have the required wire values to correctly compute our polynomial t. Instead, we will generate a random polynomial t’ and output [t’lo]1, [t’mid]1, and [t’hi]1.
In round 4, we will compute the challenge zeta and all of the evaluations as we did before, except we now use a’, b’, c’, and t’. We will then use these evaluations to construct the r polynomial in the expected way and then evaluate r at zeta and output all of the evaluations. Notice that each of the evaluations computed are consistent with the polynomials that we committed to in previous rounds.
In round 5, we will perform the calculations as expected but replace a, b, c, and t with a’, b’, c’, and t’. This is the end of the protocol, but we’re not done. The last step is to compute public input values that will trick the verifier.
Tricking the verifier really comes down to this opening proof polynomial (we can ignore the other opening proof polynomial because we zeroed out polynomial z in round 2):
Computation of opening proof polynomial (source)
Since our evaluations in round 4 corresponded to the polynomials used in round 5, the polynomial inside of the large parentheses above will evaluate to zero when evaluated at zeta; therefore, it is divisible by (X - zeta), and we can compute Wzeta. Now, we need to ensure that the values we compute in the proof are recomputed the same way by the verifier. In steps 9–11 the verifier reconstructs the values in a structure identical to how the prover calculated them. Therefore, all of these values should be valid.
This just leaves us with a final problem to solve in step 8, in which the verifier calculates t_bar. Because we output t’_bar, a random polynomial evaluated at zeta rather than the t_bar that the prover is expected to compute, the verifier’s t_bar will not match our output and will not pass the verification. However, the verifier uses public inputs to compute t_bar, which are not included in the Fiat-Shamir transformation for any of the challenges (namely, zeta). So we can retrofit our public inputs so that they force the verifier to compute t’_bar in step 8.
To do so, we first plug in the t’_bar that we computed in round 4 to the left side of the equation in step 8. Then, we solve this equation for PI(zeta), a sum over the public inputs multiplied by the Lagrangian polynomial. Since it’s a sum, there are multiple combinations that will work. The simplest way is to zero out every public input except the first and solve for the wire value that results in the PI(zeta) value we solved for. We’ve now constructed our public inputs that will trick the verifier into computing t’_bar. The reason this works is because these public input values are not used to compute zeta, so we know zeta before we have to decide on these public input values.
Now, the verifier will reconstruct the same t’_bar value that we computed in round 4, and the final pairing check will pass—we’ve successfully forged a proof.
Frozen Heart’s Impact on PlonK
Let’s take a step back and assess the severity of this vulnerability. First, let’s recall what we are proving. Using PlonK, the prover is proving to the verifier that he has correctly executed a particular (agreed upon) program and that the output he has given to the verifier is correct. In the previous section, we forged a proof by using completely random wire values for the program’s circuit. The verifier accepts this proof of computation as valid, even though the prover didn’t correctly compute any of the circuit’s wire values (i.e., he didn’t actually run the program). It’s worth reiterating that this post focused on only one kind of Frozen Heart vulnerability. Several similar attacks against this proof system are possible if other Fiat-Shamir transformations are done incorrectly.
Whether this is exploitable in practice is determined by how the verifier handles the public input values. Specifically, this is exploitable only if the verifier accepts arbitrary public inputs from the prover (rather than agreeing on them beforehand, for instance). If we look at the example code in the SnarkJS repository, we can see that the public inputs (publicSignals) are output by the prover (using the fullProve function) and blindly accepted by the verifier (this example is for Groth16, but the PlonK API works in the same way). In general, the exploitability of this vulnerability is implementation dependent.
Example code snippet using SnarkJS (source)
You can imagine that in most applications, this type of proof forgery is very severe. The PlonK proof system effectively gives zero guarantees that a program was executed correctly. Keep in mind that our example used random wire values, but this is not a requirement. A more sophisticated attacker could pick more clever wire values (e.g., by choosing an output of the program that benefits the attacker) and still perform this same attack.
This is the final post in our series on the Frozen Heart vulnerability. I hope that, by now, I’ve made it clear that these issues are very severe and, unfortunately, widespread. Our hope is that this series of posts creates better awareness of these issues. If you haven’t already, check out ZKDocs for more guidance, and please reach out to us if you’d like more content to be added!