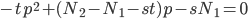今年もまた世界で一番楽しいCTF、人生でもっとも頭を高速に回転させる必要のある100分間、TSGの作問力に舌を巻く儀式であるところのTSG Live! CTFが盛大に開催されました。 今回は全然解けなくて非常に悔しい思いをしたので精進します。 それはそれとしてCryptoのwriteupを一つくらい書いておくか、ということでTwo Keysという問題のwriteupです。

問題概要

要するにの2つのRSAです

from Crypto.Util.number import *
from flag import flag

def nextPrime(n):
    while True:
        n += 1
        if isPrime(n):
            return n

class RSA:
    def __init__(self, p, q):
        assert isPrime(p) and isPrime(q)
        self.p = p
        self.q = q
        self.e = 65537
        self.d = pow(self.e, -1, (self.p-1) * (self.q-1))
    def encrypt(self, x):
        return pow(x, self.e, self.p * self.q)
    def decrypt(self, y):
        return pow(y, self.d, self.p * self.q)
    def printPublicKey(self):
        print(f"N = {self.p * self.q}")
        print(f"e = {self.e}")

p = getPrime(512)
q = getPrime(512)
pp = nextPrime(p)
qq = nextPrime(q)
rsa1 = RSA(p, q)
rsa2 = RSA(pp, qq)

x1 = int.from_bytes(str.encode(flag[:len(flag)//2]), "big")
x2 = int.from_bytes(str.encode(flag[len(flag)//2:]), "big")
y1 = rsa1.encrypt(x1)
y2 = rsa2.encrypt(x2)

assert x1 == rsa1.decrypt(y1)
assert x2 == rsa2.decrypt(y2)

print("First half:")
rsa1.printPublicKey()
print(f"y = {y1}")
print()
print("Second half:")
rsa2.printPublicKey()
print(f"y = {y2}")

解法

とりあえずは小さいことを期待して全探索することにして、からに関する式を建てます。 を開いて

です。さらになので

。両辺にをかけて整理するとという二次方程式になります。

正しいが求められていればこの式の解が整数になるはずであることを利用して探索中のが求めている値かどうかをチェックし、最終的に整数が得られれば勝ちです

exploit

時間が少ないCTFだと雑なコードを書いてしまい、結果的にタイムをロスします。丁寧にassertとか入れて仮説とその実装の正しさを保ちながらきれいに書きましょう（反省）

from gmpy2 import iroot
from tqdm import tqdm

N1 = 568...
e = 65537
c1 = 541...

N2 = 568...
e = 65537
c2 = 549...

for s in tqdm(range(10,10000)):
    for t in range(10,10000):
        a = -t
        b = N2 - N1 - s*t
        c = -s*N1

        if b**2 - 4*a*c <= 0:
            continue

        D, ok = iroot(b**2 - 4*a*c,2 )
        if not ok:
            continue
        if (-b + D) % (2*a) == 0:
            p = (-b + D) // (2*a)
            print(p)
            q = N1 // p

            pp = (p + s)
            qq = N2 // pp
            assert pp*qq == N2

            d1 = pow(e, -1, (p-1)*(q-1))
            m1 = pow(c1, d1, N1)

            d2 = pow(e, -1, (pp-1)*(qq-1))
            m2 = pow(c2, d2, N2)

            print(bytes.fromhex(hex(m1)[2:]) + bytes.fromhex(hex(m2)[2:]))

        if (-b - D) % (2*a) == 0:
            p = (-b - D) // (2*a)
            print(p)
            q = N1 // p

            pp = (p + s)
            qq = N2 // pp
            assert pp*qq == N2

            d1 = pow(e, -1, (p-1)*(q-1))
            m1 = pow(c1, d1, N1)

            d2 = pow(e, -1, (pp-1)*(qq-1))
            m2 = pow(c2, d2, N2)

            print(bytes.fromhex(hex(m1)[2:]) + bytes.fromhex(hex(m2)[2:]))

感想

この問題も他の問題も楽しかったです