今天给大家推送美国改善国家安全情报分析的行为和社会科学研究委员会;行为、认知和感知科学委员会;行为和社会科学及教育司;国家研究理事会组织编写的《情报分析》。阅读该书有利于情报分析人员了解情报分析的方法理论以及如何有效组织分析师开展情报分析工作,是情报分析理论学习中较有价值的参考资料。今天的推文将分析方法中的运筹学、博弈论、信号检测、定性分析分别推送给大家。因书本内容较多,无法逐一核对机器翻译文档。因此,后面的机器翻译文档中难免有很多错漏,请大家谅解。什么是运筹学,它是如何有用的?麻省理工学院(MIT)物理学家 Philip Morse 将运筹学定义为行动的科学研究。对行动的科学研究反映了物理科学的方法,这并不奇怪,因为运筹学的创始人是物理科学家。早期的研究侧重于通过对行动数据的分析、从第一项原则出发(往往很简单)数学模型的建立,以及设计和分析试验以检验这些模型的结果,来确立主要军事行动的物理原则。然而,随着时间的推移,数学模型的制定和分析成为运筹学研究的标志,而作为此类模型基础的数学发展到了今天,“运筹学”一词可能指与实际行动有关的数学方法。研究行动的理由不仅在于了解这些行动(这是科学调查的通常目标),而且还在于利用这种了解作出更好的行动决定。“更好”是指在组织的基本目标方面改善事务:什么决定导致更高的(如果不是最大的)利润、更低的(如果不是最小的)成本、避免的感染人数增加或成功的恐怖袭击次数减少?因此,也许更完整的行动研究的定义就是对行动的科学研究,以便作出更好的决定。对于情报分析员来说,运筹学为理解和分析某些类别的问题提供了强大的工具。然而,行动研究绝不是解决情报问题集的“一刀切”的方法。可以使用主流的思想来研究针对对手(有时是盟友)“利益系统”的行动、能力、程序的问题,而运筹学可以通过补充游戏理论等其他方法来帮助研究更关注对手意图的问题。例如,虽然运筹学的想法对于回答伊朗反对派领导人是否希望发展核武器没有多大帮助,但是这些想法可以用来估计伊朗发展核武器需要多长时间。虽然无法告诉我们,真主党是否打算在美国领土上发动攻击,但运筹学的方法可用于估计执行不同类型的攻击所需的特工数量,甚至可能估计该国境内真主党特工或同情者的数量。在将运筹学应用于情报问题时,不是期望这种方法将为无法回答的问题提供神奇的答案,而是运筹学方法可以作为连接不同信息片段的强大组织工具,并且建议感兴趣的系统的哪些未知参数对于决策是最重要的。在第二次世界大战爆发之前,英国为预期冲突所做的准备工作包括对部署新开发的雷达技术进行试验性调查,以提供预警和实时跟踪德国轰炸机攻击。到1938年中,防空演习表明,虽然雷达系统探测飞机在技术上是可行的,但"其行动成果远远达不到要求"。Bawd-sey研究站主任曾提出:应立即开始研究系统的业务方面,而不是技术方面。"行动研究"一词是为了描述这一新的努力领域。初步调查包括在编队和个别战斗中管理战斗机反击轰炸机的方法。随着战争的进行,当时的正规化(1941年)皇家空军行动科的工作人员采用统计分析、物理科学的演绎方法和常识来分析进攻和防御行动,以期减少自己的伤亡,同时给敌人造成最大的伤害。与战时行动研究有关的领先英国科学家是诺贝尔奖得主物理学家帕特里克·布莱克特,他在1940年被任命为海军运筹学主任。他参与了早期的雷达研究,并被归功于领导团队发现了商船队规模和沉没在潜艇群攻击中的商船数量之间的关系。这是英国陆军和空军进行战前雷达实验的地方。主要发现是,每次攻击中沉没的商船数量与攻击中的潜艇只数量成正比,与海军护航的数量成反比,基本上独立于船队中的商船数量。这导致建议商船组成大型船队,这反过来大大减少了北大西洋盟军运输损失。菲利普·莫尔斯被广泛认为是美国行动研究之父。1942年,莫尔斯同意参加战斗,组织一组科学家帮助美国海军研究其反潜行动。莫尔斯及其同事最初载于秘密报告和备忘录中处理的不同问题和开发的方法,已记录在《运筹学方法》中,这是该领域首次发表的文本。除了前面讨论的商船船队问题外,所报告的应用包括寻找最佳搜索模式以定位敌舰和潜艇,评估在下列情况下的权衡:•评估快速机动与防空火力对抗卡米卡泽自杀式飞机袭击;基本的物理推理(如在简单的流微分方程中捕获的)、概率建模、实验和行动(即现场)数据的统计分析,以及大量的(复杂的!)在决策过程中使用了常识。在后来的写作中,莫尔斯指出,对于运筹学人员,“任何数学领域,任何将带来结果的测量技术都被使用”“...使用这些技术的任何和所有来研究行动,以便它们可以被理解,从而被理解地控制”。另一个具有军事根源的发展已经在运筹学领域有了深刻的应用。1946年,数学家格格·丹齐格在加州大学伯克利分校休了博士学位,并在美国空军统计控制办公室工作。他面临的一个挑战是帮助空军将安排和部署部队、装备、训练和其他职能的过程标准化。这种挑战使格格·丹齐格提出线性规划问题,一种对决策问题具有广泛适用性的技术,以及求解线性程序的单纯形算法。此后,线性编程和相关的优化技术已发展成为运算研究的最大子领域之一。在二战后的几十年里,运筹学并没有孤立地发展。在工程、数学、社会和物理科学的交汇处,它与其他不断发展的学科,特别是经济学、统计学和计算机科学,分享方法、应用领域。例如,线性规划的运算研究技术对于开发博弈论中的实用解法至关重要,而博弈论又提供了经济学和政治学的基本工具。因此,运筹学演变成小组科学家使用任何可用的工具来理解和改进军事行动,或者根据情况需要开发新模型。直到第二次世界大战后,运筹研究人员才寻求专业组织和学术界的组织。1948年,运筹研究俱乐部(后来称为行动研究协会)在伦敦成立,美国行动研究协会(现称为运筹研究和管理科学研究所)于1952年成立。莫尔斯于1953年创立了麻省理工学院的运筹研究中心,并于1955年授予约翰·D·C·利特尔博士第一个博士学位。今天运筹学项目存在于世界各地的主要研究大学的工程和/或管理学校中。国际运筹研究协会联合会拥有48个活跃的国家成员协会,除了在军队中发现的应用之外,目前在公共部门和私营部门中还有大量应用。设计一个产品是一回事,但管理它的生产是另一回事。如何安排所需的生产步骤以最有效地利用现有的人力和机器?随着时间的推移,“正确”(即利润最大化)的生产水平是什么?鉴于面对不确定的最终产品需求,需要组装大量零件,并储存部分成品和成品(附带存货持有成本),库存(和什么类型)应持有多少,以及何时应下达额外供应订单?衡量质量水平和确保生产达到适当质量的最佳方法是什么?如何协调几个不同行为者(或参与者)的活动——例如供应商、制造商和零售商,每个行为者都有自己的激励措施——以便更好地协调整个供应链?这些问题和更多的问题属于制造业和供应链管理的子领域。用于调查这些问题的运营研究方法是在企业/管理学校和工业工程项目中找到的课程的标准部分(见Cachon和Terwiesch,2008年;Hopp和Spearman,2007年,介绍性文本),而主要制造公司在日常活动中依赖这种想法。
与制造业和供应链管理密切相关的是分销和物流领域,涉及"以成本效益高的方式将货物从供应源通过制造地高效率地转移至消费点,同时为客户提供可接受的服务"。为了了解分销管理中出现的问题和机遇,只需考虑联合包裹服务和联邦快递等公司的成功,这些公司围绕高效率的分销系统建立了整个业务(事实上,联邦快递被美国国防科学委员会确定为一个案例研究,以了解业务研究如何在私营部门成功制度化)。此类系统的设计和运行反映了网络流研究中的一些最著名的问题,包括运输问题(将产品从一组供应节点[或源]运输到一组需求节点[或汇]的最廉价方式是什么?)最短路径问题(如何找到给定交通网络上任何起始地点和任何目的地集合之间的最短距离?)最长路径问题(在项目管理应用中,这揭示了能够延迟所述项目的完成时间的瓶颈活动)和旅行销售人员问题(从起点出发的人必须在返回原点之前访问给定的一组位置;访问顺序将总旅行距离最小化吗?)。配送问题不限于分立机组的运输;考虑电力、石油、天然气、电子资金的流动(和定价)。服务和物理产品之间的关键区别在于服务通常同时生产和消费。客户满意度通常是由等待的经验决定的以及服务价格,是管理服务运营的一个关键目标。确定适当的服务容量(例如,服务器数量)是从呼叫中心到医院的服务中常见的问题;运筹学人员通常将排队(或等待线)理论应用于这类问题。在公共部门,业务研究人员相当重视研究和改进紧急服务,包括警察、火灾和紧急医疗服务。公共部门的其他应用包括刑事司法系统、公共交通、能源和环境。在私人部分,服务的实时定价(称为收益或收入管理)是服务管理的另一个方面,其中业务研究具有主要的效果。收入管理方法在航空公司、酒店和汽车租赁行业中经常使用。近年来,随着来自其他许多学科的学者和实践者,运筹学人员关注保健的不同方面。应用包括临床关注,例如,优化癌症的放射治疗,匹配可移植器官的供需,准备流感或其他大流行病,为艾滋病毒预防方案分配资源,以及从方案行动的角度评估具体的预防和/或治疗干预措施。关注提供医疗服务所涉及的行动是运筹学与其他研究的区别。针交换程序提供了这种观点的一个例子。这些有争议的方案使注射毒品者能够将用过的针头和注射器换成干净的针头,通过共用针头防止艾滋病毒的传播。根据这些方案的结果,一项行动研究确定了以下原则:增加针头交换率减少针头循环时间;针头在注射毒品者之间循环的时间越短,携带艾滋病毒的可能性就越小(针头由更少的人共用);以及针头中的艾滋病毒水平越低,吸毒者感染艾滋病毒的可能性较小。通过系统编码、跟踪和测试长期艾滋病毒感染交流计划中的针头,这项研究表明,这一“循环理论”的预测得到了数据的支持,结果这个社区的艾滋病毒传播大大减少。自2001年9月11日恐怖袭击以来,许多运筹研究人员把注意力转向与恐怖主义有关的问题。例子包括保护关键基础设施,如电网、管道和运输枢纽,包括机场和地铁站、化工厂、核反应堆和主要港口。已经制定了这些假设情景的模式,在许多情况下采用了建议的行动方针。其他例子包括:自杀炸弹手探测器的运作(而非科学)效能、对US-VISIT(美国国土安全部美国入境点移民和边境管理生物识别方案)进行评估并提出改进建议,以及对潜在生物恐怖袭击的准备。在制造和服务应用中,运筹研究项目所产生的货币利益,无论是通过增加收入还是降低成本,都已在具体实例中得到记录。Pringle报告了几个例子,包括:• 为Sears、Roebuck和Company工作的业务研究人员设计了一个调度系统,该系统“使一次性费用减少900万美元以及每年持续节省4 200万美元”;• Weyerhaeuser运筹学人员解决了以下问题:"在什么地方将树干切成什么长度的原木,以及应分配什么用途的原木(出口、木材、胶合板、纸张)从而节省了超过1亿美元"。•National
Car Rental的运营研究人员开发和实施了一个收入管理系统,在运营的第一年将收入提高了5600万美元。Hner谈到了Sabre的成功,Sabre是由美国航空的运营研究集团形成的分拆产品,被广泛地归功于创收管理(将实时定价与预订和调度合并)。霍纳在接受美国业务研究组织前负责人托马斯·库克(Thomas Cook)的采访时报告说,到1998年,“……美国航空公司的收入管理系统每年创收将近10亿美元。为了弄清这个数字,考虑到航空公司的总营业利润直到1997年才接近10亿美元”。业界团体产生的货币效益的其他例子出现在Bell et ai中,而Alden保守地估计,从1972年到2008年,弗兰兹·埃德尔曼奖(Franz
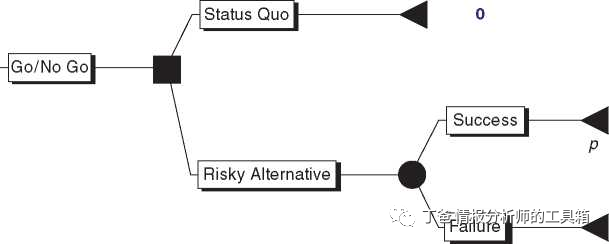
Edelman Award)决赛选手在运筹研究和管理科学方面的成就所产生的总效益超过1600亿美元,该奖项是应用运筹研究的最高奖项,每年约有六名决赛选手。运筹学人员如何从一个新的项目开始?撇开纯粹的数学研究,旨在改进运筹学的定量方法,应用研究的目标是改进决策。从历史上看,这已使行动研究小组发挥咨询作用,负责决策者(例如军事指挥官、业务主管、机构首长)请求援助,帮助改善某些方面的问题。这并不意味着问题总是出现在提出好的问题上;事实上,Mse和Kimball写道,“经常发生的是,运营研究工作者的主要贡献是决定什么是真正的问题。”后一项声明同样适用于开展研究的独立业务研究人员,以便在其感兴趣的领域取得更好的成果。理解问题通常需要理解嵌入问题的环境和/或系统。例如,可以解决的问题是:在生产过程中材料流动的基本过程;传染病爆发的传播;互联网流量的路线;罪犯通过刑事司法系统的流动;发电和分配;或在袭击途中阻截恐怖分子。这些程序的哪些部分引起关注(例如,机场或医院的过度延误)或替代地提供了机会(例如,个人支付机票、酒店房间或手机分钟费用的意愿不同)?对问题地形的基本理解使决策者和业务研究分析人员能够更有效地交流环境中的问题和/或机会。了解有关环境和/或系统需要实质性专门知识。这种专业知识通常是通过直接观察获得的,这就是为什么众所周知,业务研究人员乘坐警察巡逻车四处走动,把时间花在仓库里上,或者观察银行、高速公路、呼叫中心或迪士尼世界的线路的形成和消散。当然,在军事行动研究形成的年代里,分析人士“生活在系统中”,能够在第二次世界大战期间反复见证“问题”的新版本。开始工作的另一个重要部分就是弄清楚决策者想要实现的目标。目标是什么?如果面临两种执行有关行动的方式,决策者能否说明哪一种是首选的,为什么?让决策者在业绩计量方面明确陈述其目标是朝着理解这个问题迈出的重要一步。可能的目标/性能度量配对包括最大化利润、最小化成本、最大化节省的生命以及最小化响应时间。随着对目标和业绩计量的共同理解,问题识别变得容易得多。运筹学研究的特点是,建立一个数学模型,代表正在研究的系统的行动,以及决策者可用的选择和替代方案,这些选择和替代方案都处于适当的环境中。制作一个模型是一个创造性的行为,既是艺术,也是科学。观测和数据收集与模型开发之间的关系是双向的,因为模型可以建议像实地观测一样容易地收集新数据,从而引起所述模型的修订(或放弃)。大多数运筹学学生熟悉数学问题集,这些数学问题集旨在钻研和进一步教授正在研究的建模方法的细微差别。对实际应用程序进行建模更像是将行动情况带入现实世界,并将其分解到可以创建问题集式的问题,从而解决系统的最重要的特性和属性。尽管运算研究者在研究中采用了许多数学工具,而其他定量学科也采用了许多相同的数学技术,但是已经用识别了三组建模方法:优化、概率建模(或随机过程)和决策分析。所有这些方法已经并将继续用于前面概述的应用中。尽管感兴趣的读者可以从运筹学中的任何好的介绍性教科书中学习这些方法的基本知识,但是应当意识到,这些方法本身是数学运筹学人员中的积极研究课题,并且这些技术的新的扩展和结果继续被发现。优化问题涉及决策者控制(决策变量)下的变量的某些目标函数(例如,利润最大化、成本最小化)的最大化最小化,这取决于资源对这些变量允许值的其他约束。用于解决优化问题的技术取决于基本的数学特性(例如,目标函数是线性还是非线性,决策变量是连续值还是整数值),并且包括线性规划、非线性规划、整数规划和动态规划等。优化问题的解决方案识别在模型的假设内导致决策者的最佳结果f的决策变量的值,以及该结果的值(例如,利润最大化或成本最小化),还提供工具,用于检查这些结果(决策变量值和目标函数)对构建模型时所作假设的变化的敏感性。概率建模代表了随机性和不确定性占主导地位的行动情况;这些被称为随机过程。例如,排队理论解决了客户根据随机过程到达服务系统且服务持续时间不确定的问题。它提供了诸如客户必须等待服务多久、系统中有多少客户以及服务供应商有多忙等问题的答案;此类模型对于服务系统中的应用程序至关重要。库存理论为理解中间产品和成品在生产过程、血液/血浆供应和供应链中的流动和储存提供了额外的模型。生存分析的可靠性通过分析在患者情况下可导致整个系统故障或死亡的部件或子系统之间的相互关系,检查复杂系统例如核电站、空间系统、个体患疾病的概率。对于数学解证明太难的极为复杂的问题,仿真模型用于表示系统的行动并在计算机上生成感兴趣的数据;然后可以对所得到的数据进行统计分析,以推断系统行动与感兴趣的性能度量之间的关系。决策分析是一个混合的优化和概率方法家族,已经开发出来帮助决策者在面对随时间演变的不确定结果时评估替代行动方案。已经开发了诸如决策树和影响图之类的有用的图形工具,以表示问题环境并进一步构造此类问题。决策分析是运筹学与心理学最交叉的地方,其中判断和决策学者投入了大量精力研究个人如何实际决策(附带偏见)。另一个交汇点是经济学和政治学中的理性选择和博弈理论模型,其出发点是,个人在解决决策分析问题方面是专家,并且在战略决策中经常这样做。运筹研究的视角是咨询;鉴于决策者的偏好、对可用替代行动的了解以及对与这些替代措施相关的可能后果的估价,什么是最佳行动方案?决策分析还提供了估计关于问题可获悉的附加信息的值的方法,以便检查所建议的行动方针对于在对问题建模时作出的具体假设的敏感性(如同优化模型。上述数学方法的基础理论相当深入。因此,运筹学建模工作仅限于那些受过高级数学训练的人。然而,与假设检验和回归分析等常用统计方法一样,在应用研究中正确使用运算研究是可能的,而不必掌握所有基本的数学理论。的确,在过去十年中,运筹学方法在易于使用的电子表格软件包(例如Microsoft Excel)中被计算机化,使得制定和解决各种模型变得容易得多。同样,对看似复杂的模型的分析往往会产生一些洞察力,这些洞察力在简单性方面极其优雅,下一部分的例子就是要展示的。许多决策可以表示为“一切照旧”的状态行动模式(不去)和可能成功或不成功的风险选择(去)之间的选择。假设风险替代方案如果成功,将带来相对于现状的b个单位的增量利益(例如,额外的利润、额外的生命节省),而同样的替代方案如果失败,将造成相对于现状的c个单位的增量成本。另外,假设风险选择成功的概率等于p。这种情形在图2-1中的决策树中图示;平方表示现状与必须作出的风险备选方案之间的决策,圆表示风险备选方案的不确定性能(在树的对应“分支”上标明成功和失败的概率),与各种可能的结果相关联的增量值出现在每个分支的末尾。决策者力求使这一决定的后果预期价值最大化。与现状(当与自身相比具有预期的增量值为零时)相比,风险替代物值pxb-(0(1)-p)xc,如果p>c/(b+c),则其超过零。因此,这个模型提出了一个非常简单的规则。注意,知道成功概率p的精确值是不必要的;仅需要识别该概率是否高于低于c/(b+c)的阈值。如果递增惩罚c大大超过递增利益b,则只有当人们非常确信它将成功时,人们才应该追求危险的选择。另一方面,如果递增收益远远大于递增成本,除非人们非常确定有风险的替代方案会失败,否则“去争取”似乎是有利的。当然,与上面的简单示例相比,决策分析提供了更复杂的方法。或许与情报分析人员特别有关的是,决策分析已开发出适用于规避风险(或反过来,容易发生风险)的决策者的工具。例如,如果投掷硬币时投掷硬币,如果投掷硬币时支付0美元,如果投掷硬币时支付10美元,那么规避风险的决策者将愿意以例如4美元的价格出售该彩票的权利,即使赌博的预期价值等于5美元。相反,风险高企的决策者可能不愿意放弃这一赌博,除非至少提供6美元。决策分析提供了评估决策者是否规避风险或容易风险(或就此而言风险中立)的两种方法,以及一种详细说明此类决策者应如何选择其选项的方法。利特尔定理以麻省理工学院第一名博士生John D.C.Little命名。它指出,排队系统中的平均客户数(L)等于客户到达率(X)和在系统(W)中花费的平均时间的乘积,简单地L=XW。这个简单的公式的力量源于几乎无穷无尽的情况可以被解释为客户等待服务。例如,如果X是新产品进入特定生产阶段的速率,并且W是该生产阶段中每单位花费的平均时间,则L=XW是该生产阶段的平均生产过程库存。如果X是非法进入流通的年度枪支数量,W是非法枪支仍在使用的平均时间,则L=XW是可供使用的流通中的非法枪支的平均数量。如果X是每天起飞的飞机的平均数量,W是每次飞行花费的空中平均时间,那么L=XW是天空中飞机的平均数量。如果X是每年闲置地块的平均数量,W是从孵化新地块到成功实施或放弃/阻截地块的平均时间,那么L=XW是当前“闲置队列”中的闲置地块的平均数量。如果X是每年启动的新情报报告的平均数量,W是研究和编写报告所需的平均时间,则L=XW表示当前编写的报告的预期数量(或情报工作中的清单)。如果X是新感染艾滋病毒的年感染率,W是感染后的平均时间,在此期间,新感染者将在BED试验等专门检测最近感染证据的试验中呈现“最近感染”的结果,那么L=XW是可以被认为是新感染的人的平均人数。最近估计美国每年新艾滋病毒感染率的研究扭转了这种逻辑,方法是从感染HlV的人样本中估计L,然后通过反转利特尔定理来估计艾滋病毒感染率X。有时,仅仅因为收集数据的物理过程的差异,采样的信息在观察者之间看起来会非常不同。想象一下,在城市公交线路上,当接二连三的公交车到达和离开同一个公交车站时,会看到它们。假设9个总线之间的8个等待时间为1分钟(短间隙),但9个这样的间隔中1等于10分钟(长间隙)。现在想象一下,当公共汽车离开时,一个准乘客正好到达公共汽车站;我们的可怜的乘客实际上刚刚错过公共汽车。这位乘客在下班车前等待10分钟的可能性有多大?很显然,答案等于1/9,就像在公交车之间的所有间隔中,9分之一的构造等于10分钟。现在假设第二位准乘客到达同一公共汽车站,但到达时相对于公共汽车是随机的。这位乘客面对10分钟间隔的机会是多少?答案不再等于1/9;随机到达的乘客有5/9的机会在长空降落!原因是到达给定长度的间隙的机会与产生这种间隙的频率和间隙持续时间成比例。因此,到达长间隙的机会与(1/9)x10成比例,而到达短间隙的机会与(8/9)x1成比例,从而产生在等于(10/9)/(10/9+8/9)=5/9的长间隙期间到达的概率。情况甚至比这更奇怪:刚错过公共汽车的第一名乘客必须等待1x 8/9+10x 1/9=2分钟的下一班公共汽车,而第二名乘客平均等待(10/2)x
5/9+(1/2)x 4/9=3分钟,在这个例子中,刚错过公共汽车的人面临的等待时间比随机时间到达的人要短。这是一个运筹学人员称之为随机发生率(或统计用语中的长度偏向抽样)的例子。它可以解释为什么不同的人观察相同的现象会看到不同的东西。例如,如果对研究感染疾病的人的进展感兴趣,则通过随着时间的推移跟踪新感染者,而不是在医院对患有相同疾病的病人进行采样,并且随着时间的推移跟踪他们,可以获得不同的图像。同样,对失业时间的研究显示,与目前领取失业保险者的随机抽样相比,新失业者的抽样结果大不相同。一个常见的优化问题是在不同的活动中分配预算。例如,由于固定预算用于不同的保健方案,政府应该拨出多少钱用于不同的护理和预防活动?产生实际分配规则的这类问题的一个模型是背包模型。在这个模型中,一些可能的活动(或方案)可以得到资金。让bi和ci分别表示zth活动的单位益处和成本(例如,每个单位可以c响应递增的雇员设施),并且假设存在对允许的活动单位数量的上限(例如,由于节目容量,或者可能由于限制任何单个节目可以接收的资金量的政治原因)。目标是在给定预算内尽量扩大总体效益,解决方案特别简单。首先,将活动从“砰砰”的比率bjc^的最大值到最小值排序,然后,以该比率最高(即总预算和最大允许金额中的较小值)为该活动分配可能的最大金额。这项活动在所有活动中产生的每美元效益最大,因此是产生效益的最具成本效益的手段。接下来,考虑减去授予最高效率项目的金额后剩余的预算,并转移到降压率第二高的活动。再次,分配尽可能多的资金,更新预算,并转移到下一个最有效的活动。以这种方式继续下去,直到所有活动全部获得资金为止,剩余预算用尽,同时为目前列为最高效的任何活动提供资金(在这种情况下,这项活动只能获得部分资金)。在这项工作结束时,将有一套资金完全到位的活动(那些对美元比率影响最大的活动)、一套没有获得资金的活动,以及可能还有一项获得部分资金的活动。当然,部分资金是不可能的——例如,建造半座坦克三分之二的桥梁可能价值不大。在这种情况下,复杂的优化技术可用于确保所有被资助的活动被完全资助(例如,整数或动态规划)。这个问题最重要的方面是解决方案背后的直觉:将资源按最大到最低效率的活动顺序分配,即从最大到最小的代价分配。在艾滋病毒预防的例子中,这项规则规定,预防方案应按每美元预防感染最多至最少的顺序供资。虽然资源分配问题通常比简单的背包公式更复杂,但是在考虑效率较低的替代方案之前为更有效的活动和方案争取资金的原则通常提供良好的启发。项目经理面临的一个常见问题是安排完成项目必须完成的各种活动。“项目”一词可作相当宽泛的解释,例如建筑项目、筹资运动、武器开发项目以及恐怖袭击。其中一个最重要的问题是完成整个项目需要多长时间?回答这个问题的一个简单方法是:首先,生成必须完成的所有项目任务的列表,以及每个任务持续时间的估计。第二,对于每一项任务,请注意必须在有关任务开始前立即完成的“直接前任”活动。第三,从没有必备活动的任务开始(因此项目启动时可以在“零时”开始),确定最早完成这些活动的时间。这些都是“第一轮”活动,因为它们的完成并不依赖其他活动,它们的“早期完成”时间只是任务的持续时间。第四,对于每个剩余的下游任务,从公式计算每个任务能够开始的最早时间:其中,最高值被接管所有早期完成时代的任务的前任。这些早期完成时间计算为:注意,没有先决条件活动的第一轮活动都具有零的早期开始时间,而具有直接前人的第二轮任务将具有从上述两个公式中的第一个确定的早期开始时间。递归地应用这些步骤直到所有任务都已经被解决,就会产生整个项目的持续时间。这种“关键路径方法”还确定了那些如果推迟,会延缓整个项目完成的活动。对于项目管理员来说,这些关键活动是必须加速开展的活动。或者,在敌对情况下,人们希望阻碍敌方项目的进展,拖延例如策划恐怖袭击等关键活动,可能会拖延整个项目。我介绍了一个高度简化的项目日程安排,可以更加现实。例如,任务持续时间不太可能确切地知道;更先进的模型将这些持续时间作为随机变量处理,使得人们能够计算项目在给定日期之前完成的概率。或者,可以专注于成本/完成权衡,以研究在快速预算下完成项目的速度。运筹学研究与情报分析具有至少两个共同特征。首先,正如《情报comnmity指令》(情报界(Intelligence Community)指令分析标准所述,情报分析人员预计“从无偏见的角度”和“独立于政治考虑”履行其分析和信息职能”。情报分析员不做决定,而是提供信息支持政府(或军事)执行决策者。业务研究人员同样在行政决策者方面扮演无偏见分析师的咨询角色。关于分离运筹学支持和执行决策的写作,Mse和Kimball指出,“要求行政部门就某项行动作出决定,在某种程度上与要求他按照行动研究的要求,科学和客观地看待这项要求相抵触”(着重部分由作者标明)。第二个共同关心的问题是及时性;《分析标准指令》指出,“分析产品迟迟不能支持消费者的工作,会削弱效用和影响力。分析师将努力及时交付产品,以便客户能够采取行动”。写半个多世纪前,莫尔斯和Kimball指出,“运筹研究和其他科学工作的一个重要区别是所涉及的紧迫感。在这一领域,基于不完整数据的初步分析往往比使用适当数据进行更彻底的研究更有价值,这仅仅是因为关键的决定不能等待较慢的研究,而必须基于初步分析。大的改进通常来自对新领域的第一次快速调查;后来的详细研究可能只获得小的额外因素。”考虑到的军事以及情报分析的军事和系统方面,运筹研究偶尔被用于情报分析是不足为奇的。例如,Caldwell报告了“评估情报系统产出的模型”,目的是了解不同情报对情报评估总体价值的相对贡献。Steele使用运筹学模型来说明当目标是保密时,不同通信协议带来的优缺点。然而,在情报分析中经常应用运筹学的证据很难找到。Heuer、Schum、Schum和Mris和Zlotnick都讨论了基本概率模型的使用,包括贝叶斯规则,目的是评估各种事件或“事态”的可能性,但是没有关注这种以其他方式吸引人的工作的行动。在国家情报机构发布的情报分析引文中,几乎完全没有行动构想。事实上,与优秀的军事资源(如海军研究生院的运筹学小组和军事行动研究协会)形成对照的是,除了在国家安全局(National Security Agency,National Security
Agency)发现的运筹学方面的重点技术专长,在情报界(Intelligence Community)内工作的运筹学人员显然很少。不建议情报分析人员掌握 ,就有机会通过适当应用行动研究改进情报分析。当情报分析人员专注于对敌对的供应链、武器开发项目、恐怖袭击的规划、人员或物资的分配,或任何其它感兴趣的行动作出推论时,这些的调节就出现了。此外,正如在利特尔定理的应用中,最初可能不构成行动的问题有时可以被理解为这样的问题。以下例子旨在说明将运筹研究应用于情报问题的机会。核武器的发展为将运筹学应用于情报问题提供了一个有趣的案例研究。在询问是不是“扩散者”正在推行核武器计划时,重要的是要了解一个旨在生产此类武器的项目可能采取的形式。对这一问题的行动研究(或)方法侧重于查明除了武器生产过程本身之外武器生产所需的基础设施任务,并认真注意这些任务的必要顺序和时间安排。可以使用前面描述的关键路径方法的更复杂的版本来处理这样的项目管理和调度问题。Harney恰好报告了这样一项研究。设计这种武器所需的基本科学资料已广为人知并公开已有相当一段时间。利用这一来源和其他来源,Harney和同事们能够估计,根据关于资源可得性的假设(例如,现有预算,无论是生产还是立即提供[即被盗或购买]),完成第一批六件武器所需的时间为4至6.5年。在一篇同伴论文中,相同的研究人员询问项目网络中的哪些任务如果延迟,将最大程度地推迟武器开发项目。在许多不同的情况下,作者确定了两个瓶颈任务(“级联装载”和“获取泵和管道”),即如果被拦截,如果扩散者不知道拦截行动(完美的隐蔽行动),生产武器的持续时间将增加37%。即使增殖者知道阻截努力并相应地修改生产过程(如使用博弈论建模),阻截这些活动仍然可以将整个项目延迟34%。同样,这个想法并不是这个模型告诉情报分析员亲生者的核武器计划的确切状态,但它确实表明,哪些生产活动对整个发展项目至关重要,因此哪些参数可能值得更加集中的情报努力。估计隐藏种群的大小是许多领域的共同问题。公共卫生官员希望了解新感染艾滋病毒的人数,野生动物管理者希望了解各种动物的大小植物,以及执法、药物治疗方面的决策者和专业人员,和公共卫生要求估计注射毒品者的人数。同样,未知数量的未发现的恐怖分子(或恐怖阴谋)对反恐、执法和国土安全决策者有着极大的兴趣。尽管来自卧底特工机密线人的人力情报(HUMINT)在中断特定阴谋中起到了至关重要的作用(缺乏这种情报是9/11之前经常提到的失败),但行动研究为从卧底活动和利用数据中估计未被发现的恐怖阴谋的数量提供了机会。利用排队论可以表征恐怖袭击的煽动和规划与秘密情报人员的使用之间的关系。将恐怖阴谋视为“客户”,将卧底特工视为“服务器”,排队理论允许人们基于服务器的利用率来估计等待客户的数量,其方式类似于人们如何从呼叫中心的服务器利用率来估计等待客户的数量。恐怖分子侦查过程的一个重要特点是,与大多数服务系统的客户不同,恐怖分子不希望得到“服务”,而且会泄露虚假信息,使反恐调查人员偏离轨道,卧底特工和线人犯了“假阳性”错误,导致在寻找假线索时浪费时间。希望采用所建议的形式模式能够提供一种办法,从一系列情报报告中推断恐怖主义活动的总体水平,否则这些情报报告只针对有关具体个人的信息加以研究。从这一想法而来的其他应用包括确定用于秘密情报收集的适当资源量,评估对人力资源的投资与改进的检测技术之间的权衡。最近发展了一种不同的追踪恐怖威胁的方法,其基础是概率理论和项目管理。正如Godfrey和Mifflin和Godfrey所报告的,执行恐怖攻击所需的各种活动可以以项目网络的形式组织,同时仔细注意任务之间的优先关系和每个任务持续时间的估计概率分布。考虑到对不同任务状况的情报评估,这个TerrAlert模型对攻击发生之前的剩余时间进行评估。它还建议中断哪些项目任务以最大限度的延迟。引述作者,“例如,在我们怀疑正在执行制造任务的工厂进行轰炸时,最有效,当任务尚未启动时,效果较差(原料可以改道到另一个设施),当任务完成时(最终产品已经生产和分发)无效”。美国国防威胁减少局(Defense
Threat Reduction Agency)和海军情报局(Office of Naval
Intelligence)高级海事分析小组(Advanced Maritime Analysis Cell)已经安装了TerrAlert,不过目前使用状况尚不清楚。在情报分析中,最根本的问题可能是“连接点”,意思是“……选择和收集不同的信息,以便对威胁有一个普遍的理解……”。将数据挖掘等统计工具直接应用于记录旅行金融交易的大型数据库,必然会遇到搜索数据库后出现的假阳性问题,在这些数据库中,参与恐怖主义的个人的基本比率极低。甚至专门用于追踪恐怖分子的系统也遭受这种低基率问题。例如,在2004年7月至2007年11月期间,联邦调查局(FBEs)恐怖主义威胁和可疑事件追踪系统(称为“卫报”)收到了大约108,000份关于潜在恐怖威胁和可疑事件的报告,然而FBI断定,绝大多数报告与恐怖主义无关。解决这一问题的作业研究方法,首先应慎重地构建情报数据收集和报告之间当前关系的简单化模型,以及经验丰富的情报分析人员如何处理这类数据,以便生成和测试新的假设,并评估(在模型内)这一当前方法的成功。只有在了解当前关系之后,才能尝试使用运筹学方法来改进结果(在当前面临的相同资源约束内连接更多点)。情报分析的产生本身可以被看作一个以不同类型的反复行动为特征的过程。例如,在宏观一级,人们可以问“情报周期”——需求规划、数据收集、数据处理和利用、情报分析和情报报告的编制,向政府军事决策者(“消费者”)传播产品和产品是平衡的,因为总体情报预算已经适当地分配在这些不同的活动中,以最大化整个系统产生的情报的价值。例如,国防科学委员会考虑了以下关于伴随无人机系统(UAS)的昂贵的新生物特征数据收集能力的潜在业务研究应用:“技术可用于分析整个ISR9系统有效使用预期新收集能力的能力和/或理解哪些额外成本将具有情报、监视和侦察。一个明显的例子是,是否对分析资源(具体技能、招聘和培训)和传播能力进行了不适当的投资,以应付无人机系统(UAS)投资生产的新产品的数量。作为另一个例子,考虑将情报分析员分配到不同的感兴趣地理区域,分配到不同的情报问题集。将工人分配给任务构成被称为分配问题的经典运筹学模型的基础。基于分配模型的分配应该导致情报范围/专门知识和分析任务之间更好的总体匹配,而不是简单地在现有基础上向最佳可用分析员分配任务。这和以前的例子都表明,把创造情报本身看作一种生产过程,本身就证明是一种有益但具有挑战性的运筹学的应用。![]()
![]()
文章来源: http://mp.weixin.qq.com/s?__biz=MzI2MTE0NTE3Mw==&mid=2651131872&idx=1&sn=6dbee9e0f006b7bd4b02d0edc44c9bf1&chksm=f1af78dac6d8f1cc91ad787e54f9c2f0eee0810c223c4cf6c32047b0eef217da25556e0e4a6b#rd
如有侵权请联系:admin#unsafe.sh
