
2023-7-4 10:25:0 Author: www.cnblogs.com(查看原文) 阅读量:13 收藏
预期收益是
强化学习中的核心优化问题可以表示为:

5、值函数(Value Function)
知道一个状态的值或者状态行动对(state-action pair)很有用。这里的值指的是,如果你从某一个状态或者状态行动对开始,一直按照某个策略运行下去最终获得的期望回报。几乎是所有的强化学习方法,都在用不同的形式使用着值函数。
这里介绍四种主要函数:
- 同策略值函数:
,从某一个状态s开始,之后每一步行动都按照策略π执行
-
同策略行动-值函数:
,从某一个状态s开始,先随便执行一个行动a(有可能不是按照策略走的),之后每一步都按照固定的策略执行π
-
最优值函数:
,从某一个状态s开始,之后每一步都按照最优策略π执行
- 最优行动-值函数:
,从某一个状态s开始,先随便执行一个行动a(有可能不是按照策略走的),之后每一步都按照最优策略执行π
全部四个值函数都遵守自一致性的方程叫做贝尔曼方程,贝尔曼方程的基本思想是:
起始点的值等于当前点预期值和下一个点的值之和。
同策略值函数的贝尔曼方程:
最优值函数的贝尔曼方程是:
同策略值函数和最优值函数的贝尔曼方程最大的区别是是否在行动中去max。这表明智能体在选择下一步行动时,为了做出最优行动,他必须选择能获得最大值的行动。
举例来说,在象棋游戏中,定义赢得游戏得1分,其他动作得0分,状态是棋盘上棋子的位置。仅从1分和0分这两个数值并不能知道智能体在游戏过程中到底下得怎么样,而通过价值函数则可以获得更多洞察。
价值函数使用期望对未来的收益进行预测,一方面不必等待未来的收益实际发生就可以获知当前状态的好坏,另一方面通过期望汇总了未来各种可能的收益情况。使用价值函数可以很方便地评价不同策略的好坏。
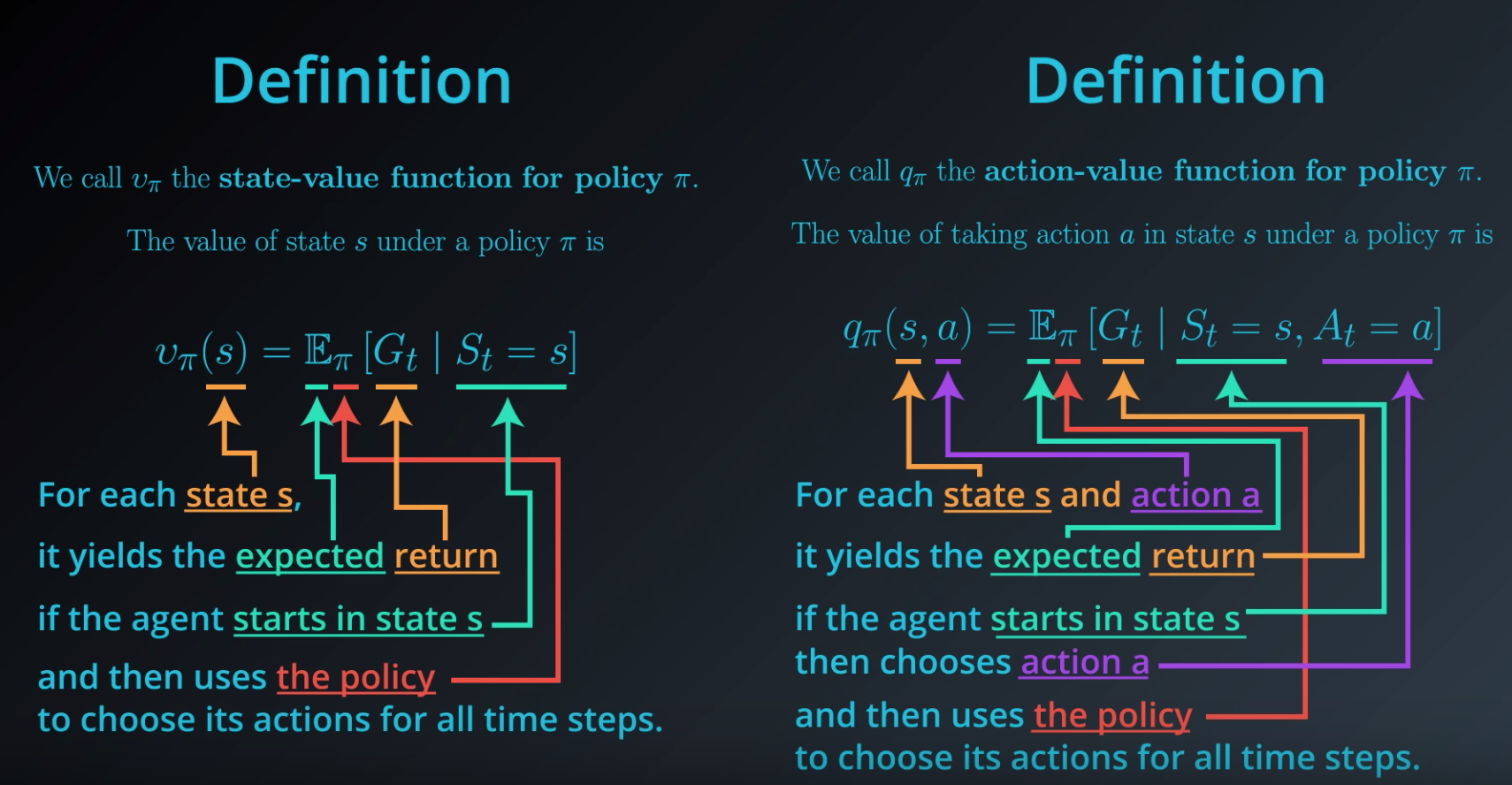
- 状态价值函数(State-value Function):用来度量给定策略π的情况下,当前状态St的好坏程度。
- 动作价值函数(Action-value Function):用来度量给定状态St和策略π的情况下,采用动作at的好坏程度。
6、最优 Q 函数和最优行动
最优行动-值函数

最优策略s会选择从状态s开始选择能够最大化期望回报的行动。所以如果我们有了

注意:可能会有多个行为能够最大化
7、优势函数(Advantage Functions)
强化学习中,有些时候我们不需要描述一个行动的绝对好坏,而只需要知道它相对于平均水平的优势。也就是说,我们只想知道一个行动的相对优势 。这就是优势函数的概念。
一个服从策略π的优势函数,描述的是它在状态s下采取行为a比随机选择一个行为好多少(假设之后一直服从策略π)。数学角度上,优势函数的定义为:
0x2:强化学习中的六类问题
虽然强化学习给出了一个非常通用的解决问题的思路,但是面对具体问题,在不同场景下,强化学习又会有不同的侧重。这些侧重点主要体现在一下六类问题的不同探索点上:
- Learning:如何通过学习去解决问题,智能体从未知的环境中通过策略学习提高。
- Planing:如何通过规划去解决问题,已知基于环境的模型,智能体通过模型进行计算,并且不需要外部交互,智能体能够提高策略的表现。这类问题的典型案例是 alphaGo。在已知围棋的规则下,去寻找最优结果。
- Explorition:如何通过探索去解决问题,智能体通过试错获取环境信息。
- Exploitation:如何利用已知信息去解决问题,智能体利用获取的信息获取最大奖励。
- Prediction:如何借助预测未来去解决问题,通过评估和预测未来,给出最佳策略。
- Control:如何通过控制未来去解决问题,通过控制和改变未来,找到最佳策略。
六类问题本身并不独立,我们在这里把六类问题抽象出来看,每类问题下都有很多经典的应用。
0x3:强化学习的数学模型
本质上,所有强化学习算法,都可以抽象为如下的标准数学形式:
马尔科夫决策过程(Markov Decision Processes, MDPs)。MDP是一个5元组
马尔科夫决策过程指的是服从马尔科夫性的系统:
状态转移只依赖与最近的状态和行动,而不依赖之前的历史数据。
0x4:强化学习中的算法
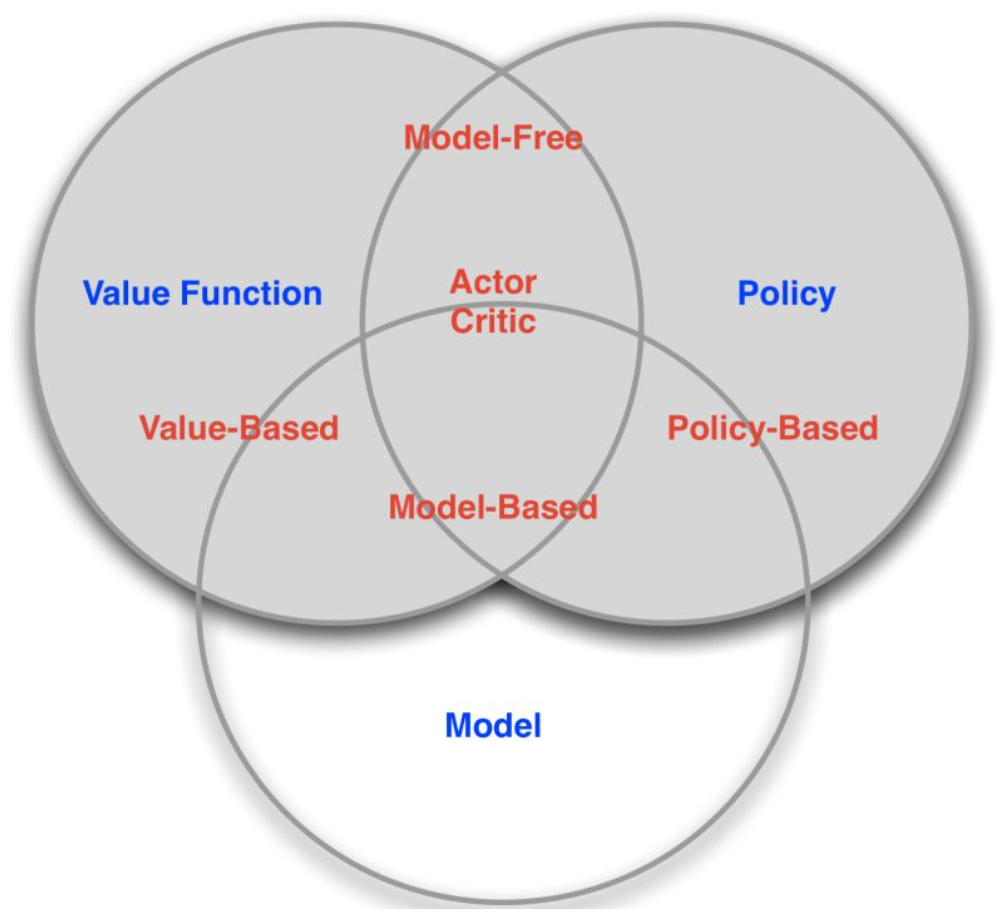
有了上述六类问题,我们再看看如何通过方法或者方法的组合去定义解决问题的算法。
基于是否使用了Policy、Value fuction、Model 不同的方法组合,强化学习算法可以分为
- 按照环境是否已知划分
-
免模型学习(Model-Free):Model-free就是不去学习和理解环境,环境给出什么信息就是什么信息,常见的方法有policy optimization和Q-learning
- 有模型学习(Model-Based):Model-Based是去学习和理解环境,学会用一个模型来模拟环境,通过模拟的环境来得到反馈。Model-Based相当于比Model-Free多了模拟环境这个环节,通过模拟环境预判接下来会发生的所有情况,然后选择最佳的情况。
-
- 按照学习方式划分:
- 在线策略(On-Policy):是指agent必须本人在场, 并且一定是本人边玩边学习。典型的算法为Sarsa。
- 离线策略(Off-Policy):是指agent可以选择自己玩, 也可以选择看着别人玩, 通过看别人玩来学习别人的行为准则, 离线学习同样是从过往的经验中学习, 但是这些过往的经历没必要是自己的经历, 任何人的经历都能被学习,也没有必要是边玩边学习,玩和学习的时间可以不同步。典型的方法是Q-learning,以及Deep-Q-Network。
- 按照学习目标划分:
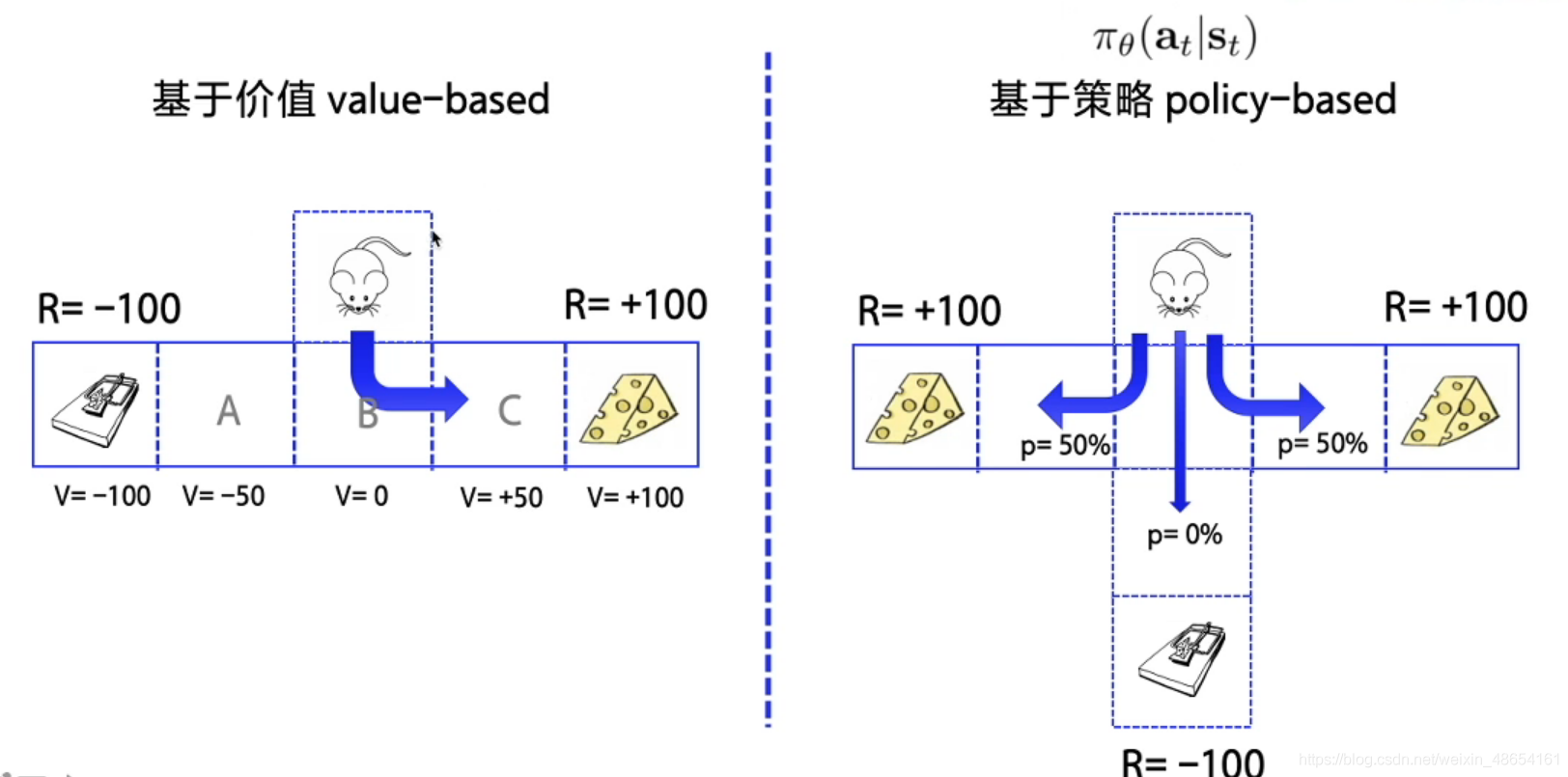
- 基于策略(Policy-Based):直接输出下一步动作的概率,根据概率来选取动作。但不一定概率最高就会选择该动作,还是会从整体进行考虑。适用于非连续和连续的动作。常见的方法有Policy gradients。
- 基于价值(Value-Based):输出的是动作的价值,选择价值最高的动作。适用于非连续的动作。常见的方法有Q-learning、Deep Q Network和Sarsa。
- 更为厉害的方法是二者的结合:Actor-Critic,Actor根据概率做出动作,Critic根据动作给出价值,从而加速学习过程,常见的有A2C,A3C,DDPG等。

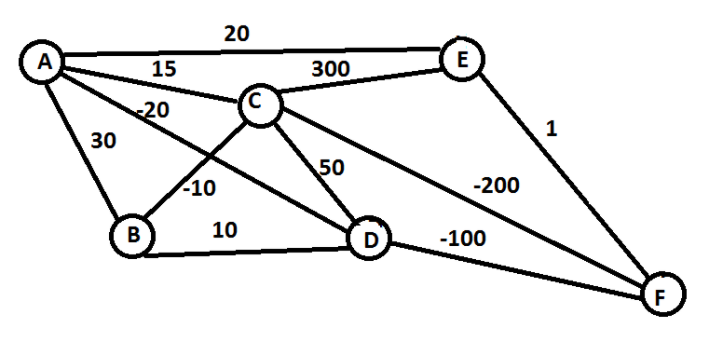
一般情况下,环境都是不可知的,所以学术和工业界主要研究无模型问题。我们可以用一个最熟知的旅行商例子来看,
我们要从 A 走到 F,每两点之间表示这条路的成本,我们要选择路径让成本越低越好:
对应到强化学习语境下几大元素分别是:
- states:节点 {A, B, C, D, E, F}
- action:从一点走到下一点 {A -> B, C -> D, etc}
- reward function:边上的 cost
- policy:完成任务的整条路径 {A -> C -> F}
有一种走法是这样的,
在 A 时,可以选的 (B, C, D, E),发现 D 最优,就走到 D,此时,可以选的 (B, C, F),发现 F 最优,就走到 F,此时完成任务。
这个算法就是强化学习的一种,叫做 epsilon greedy,是一种 Policy based 的方法,当然了这个路径并不是最优的走法(最优走法应该是A -> C -> F)。
此外还可以从不同角度使分类更细一些:
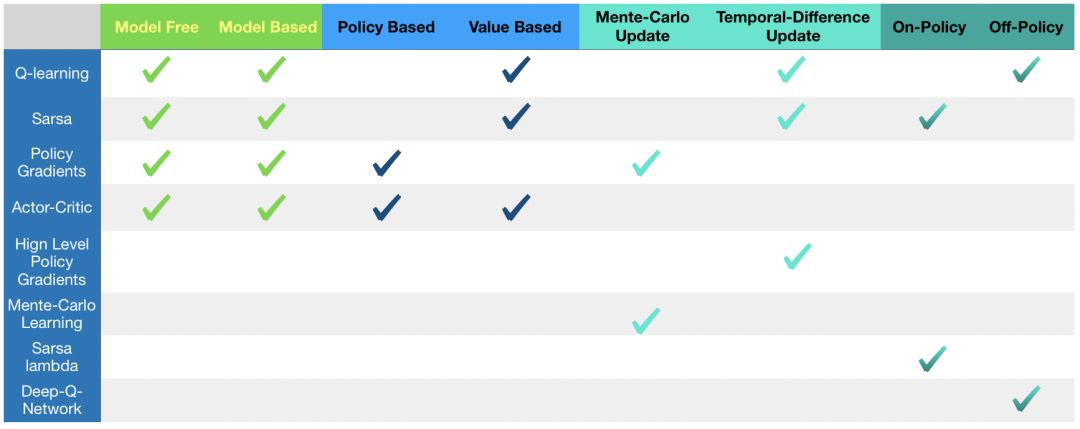
- Model-free:不尝试去理解环境, 环境给什么就是什么,一步一步等待真实世界的反馈, 再根据反馈采取下一步行动。
- Model-based:先理解真实世界是怎样的, 并建立一个模型来模拟现实世界的反馈,通过想象来预判断接下来将要发生的所有情况,然后选择这些想象情况中最好的那种,并依据这种情况来采取下一步的策略。它比 Model-free 多出了一个虚拟环境,还有想象力。
- Policy based:通过感官分析所处的环境, 直接输出下一步要采取的各种动作的概率, 然后根据概率采取行动。
- Value based:输出的是所有动作的价值, 根据最高价值来选动作,这类方法不能选取连续的动作。
- Monte-carlo update:游戏开始后, 要等待游戏结束, 然后再总结这一回合中的所有转折点, 再更新行为准则。
- Temporal-difference update:在游戏进行中每一步都在更新, 不用等待游戏的结束, 这样就能边玩边学习了。
- On-policy:必须本人在场, 并且一定是本人边玩边学习。
- Off-policy:可以选择自己玩, 也可以选择看着别人玩, 通过看别人玩来学习别人的行为准则。
0x5:强化学习与监督学习、非监督学习的区别
强化学习是除了监督学习和非监督学习之外的第三种基本的机器学习方法。
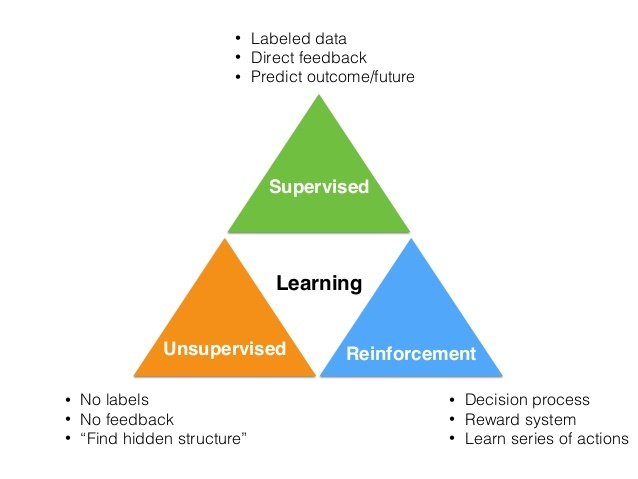
- 监督学习 是从外部监督者提供的带标注训练集中进行学习。 (任务驱动型)
- 非监督学习 是一个典型的寻找未标注数据中隐含结构的过程。 (数据驱动型)
- 强化学习 更偏重于智能体与环境的交互, 这带来了一个独有的挑战 ——“试错(exploration)”与“开发(exploitation)”之间的折中权衡,智能体必须开发已有的经验来获取收益,同时也要进行试探,使得未来可以获得更好的动作选择空间。 (从错误中学习)
强化学习主要有以下几个特点:
- 试错学习:强化学习一般没有直接的指导信息,Agent 要以不断与 Environment 进行交互,通过试错的方式来获得最佳策略(Policy)。
- 延迟回报:强化学习的指导信息很少,而且往往是在事后(最后一个状态(State))才给出的。比如 围棋中只有到了最后才能知道胜负。
1、强化学习和监督式学习的区别
- 监督式学习就好比你在学习的时候,有一个导师在旁边指点,他知道怎么是对的怎么是错的(任务驱动型),但在很多实际问题中,例如 chess,go,这种有成千上万种组合方式的情况,不可能有一个导师知道所有可能的结果。
- 而这时,强化学习会在没有任何标签的情况下,通过先尝试做出一些行为得到一个结果,通过这个结果是对还是错的反馈,调整之前的行为,就这样不断的调整,算法能够学习到在什么样的情况下选择什么样的行为可以得到最好的结果。就好比你有一只还没有训练好的小狗,每当它把屋子弄乱后,就减少美味食物的数量(惩罚),每次表现不错时,就加倍美味食物的数量(奖励),那么小狗最终会学到一个知识,就是把客厅弄乱是不好的行为。
两种学习方式都会学习出输入到输出的一个映射,
- 监督式学习出的是之间的关系,可以告诉算法什么样的输入对应着什么样的输出。
- 强化学习出的是给机器的反馈 reward function,即用来判断这个行为是好是坏。
另外它们在反馈闭环时效性方面也不一样,
- 强化学习的结果反馈有延时,有时候可能需要走了很多步以后才知道以前的某一步的选择是好还是坏。
- 而监督学习做了比较坏的选择会立刻反馈给算法。
同时它们的输入分布也不一样,
- 而且强化学习面对的输入总是在变化,每当算法做出一个行为,它影响下一次决策的输入。
- 而监督学习的输入是独立同分布的。
通过强化学习,一个 agent 可以在探索和开发(exploration and exploitation)之间做权衡,并且选择一个最大的回报。
- exploration 会尝试很多不同的事情,看它们是否比以前尝试过的更好。
- exploitation 会尝试过去经验中最有效的行为。
一般的监督学习算法不考虑这种平衡,就只是是 exploitative。
2、强化学习和非监督式学习的区别
非监督式不是学习输入到输出的映射,而是模式(数据驱动型)。例如在向用户推荐新闻文章的任务中,非监督式会找到用户先前已经阅读过类似的文章并向他们推荐其一,而强化学习将通过向用户先推荐少量的新闻,并不断获得来自用户的反馈,最后构建用户可能会喜欢的文章的“知识图”。
3、强化学习和自监督学习的区别
自监督学习将输入和输出当成一个完整的整体,它通过挖掘输入数据本身提供的弱标注信息,基于输入数据的某些部分预测其它部分。在达到预测目标的过程中,模型可以学习到数据本身的语义特征表示,这些特征表示可以进一步被用于其他任务当中。
Yan Lecun认为自监督学习(Self-supervised learning)可以作为强化学习的一种潜在解决方案,因为自监督学习将输入和输出都当成完整系统的一部分,使得它在诸如图像补全,图像迁移,时间序列预测等任务上都非常有效。此外自监督模型的复杂度随着额外反馈信息的加入而增加,可以在很大程度上减少计算过程中人为的干预。
深度学习方法在计算机视觉领域所取得的巨大成功,要归功于大型训练数据集的支持。这些带丰富标注信息的数据集,能够帮助网络学习到可区别性的视觉特征。然而,收集并标注这样的数据集通常需要庞大的人力成本,而所标注的信息也具有一定的局限性。作为替代,使用完全自监督方式学习并设计辅助任务来学习视觉特征的方式,已逐渐成为计算机视觉社区的热点研究方向。
简言之,自监督学习是一种特殊目的的无监督学习。不同于传统的AutoEncoder等方法,仅仅以重构输入为目的,而是希望通过surrogate task学习到和高层语义信息相关联的特征。
参考链接:
https://easyai.tech/ai-definition/reinforcement-learning/ https://mp.weixin.qq.com/s/84ZN_ctsWsjZSinZmJflRg https://spinningup.readthedocs.io/zh_CN/latest/spinningup/rl_intro.html https://www.youtube.com/watch?v=vmkRMvhCW5c https://stepneverstop.github.io/%E5%BC%BA%E5%8C%96%E5%AD%A6%E4%B9%A0%E5%9F%BA%E6%9C%AC%E6%A6%82%E5%BF%B5.html https://blog.csdn.net/weixin_45560318/article/details/112981006 https://leovan.me/cn/2020/05/introduction-of-reinforcement-learning/ https://github.com/dennybritz/reinforcement-learning https://github.com/openai/baselines https://easyai.tech/ai-definition/reinforcement-learning/
0x1:游戏
- 2016年:AlphaGo Master 击败李世石,使用强化学习的 AlphaGo Zero 仅花了40天时间,就击败了自己的前辈 AlphaGo Master。《被科学家誉为「世界壮举」的AlphaGo Zero, 对普通人意味着什么?》
- 2019年1月25日:AlphaStar 在《星际争霸2》中以 10:1 击败了人类顶级职业玩家。《星际争霸2人类1:10输给AI!DeepMind “AlphaStar”进化神速》
- 2019年4月13日:OpenAI 在《Dota2》的比赛中战胜了人类世界冠军。《2:0!Dota2世界冠军OG,被OpenAI按在地上摩擦》
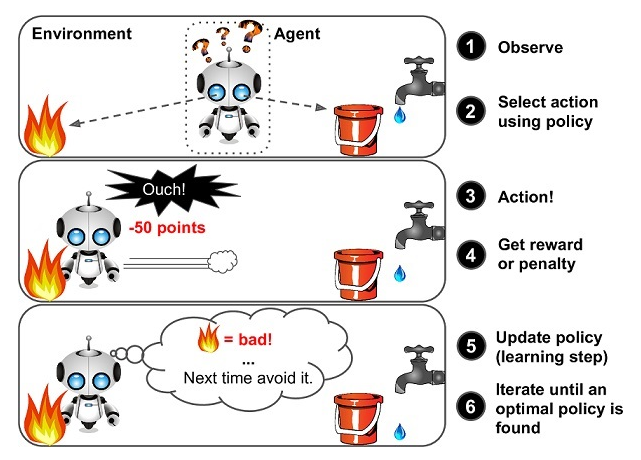
强化学习算法的思路非常简单,以游戏为例,如果在游戏中采取某种策略可以取得较高的得分,那么就进一步「强化」这种策略,以期继续取得较好的结果。这种策略与日常生活中的各种「绩效奖励」非常类似。
在 Flappy bird 这个游戏中,我们需要简单的点击操作来控制小鸟,躲过各种水管,飞的越远越好,因为飞的越远就能获得更高的积分奖励。这就是一个典型的强化学习场景:
- 机器有一个明确的小鸟角色——代理
- 需要控制小鸟飞的更远——目标
- 整个游戏过程中需要躲避各种水管——环境
- 躲避水管的方法是让小鸟用力飞一下——行动
- 飞的越远,就会获得越多的积分——奖励

0x2:机器人
机器人很像强化学习里的「代理」,在机器人领域,强化学习也可以发挥巨大的作用。
- 《机器人通过强化学习,可以实现像人一样的平衡控制》
- 《深度学习与强化学习相结合,谷歌训练机械臂的长期推理能力》
- 《伯克利强化学习新研究:机器人只用几分钟随机数据就能学会轨迹跟踪》
- Manufacturing:例如一家日本公司 Fanuc,工厂机器人在拿起一个物体时,会捕捉这个过程的视频,记住它每次操作的行动,操作成功还是失败了,积累经验,下一次可以更快更准地采取行动。
0x3:产业领域
强化学习在推荐系统,对话系统,教育培训,广告,金融等领域也有一些应用:
- 《强化学习与推荐系统的强强联合》
- 《基于深度强化学习的对话管理中的策略自适应》
- 《强化学习在业界的实际应用》
- Customer Delivery:制造商在向各个客户运输时,想要在满足客户的所有需求的同时降低车队总成本。通过 multi-agents 系统和 Q-learning,可以降低时间,减少车辆数量。
- Financial Investment Decisions:例如这家公司 Pit.ai,应用强化学习来评价交易策略,可以帮助用户建立交易策略,并帮助他们实现其投资目标。
参考链接:
https://blog.csdn.net/qq_39521554/article/details/80715615
总体来说,强化学习算法可以分为两大流派,即
- 免模型学习(Model-Free)
- 有模型学习(Model-Based)
这2个分类的重要差异是:智能体是否能完整了解或学习到所在环境的模型。
- 有模型学习(Model-Based)对环境有提前的认知,可以提前考虑规划,但是缺点是如果模型跟真实世界不一致,那么在实际使用场景下会表现的不好。
- 免模型学习(Model-Free)放弃了模型学习,在效率上不如前者,但是这种方式更加容易实现,也容易在真实场景下调整到很好的状态。所以免模型学习方法更受欢迎,得到更加广泛的开发和测试。
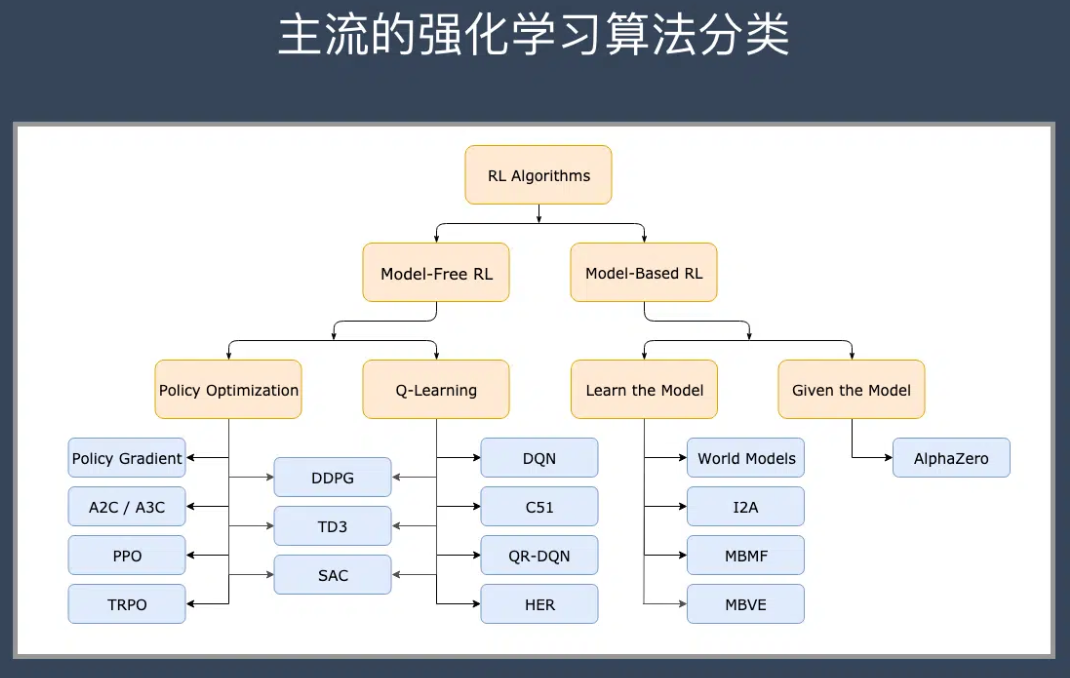
0x1:免模型学习
1、策略优化(Policy Optimization)
这个系列的方法将策略表示为
![]()
它们直接对性能目标![]() 进行梯度下降进行优化,或者间接地,对性能目标的局部近似函数进行优化。
进行梯度下降进行优化,或者间接地,对性能目标的局部近似函数进行优化。
系统会从一个固定或者随机起始状态出发,策略梯度让系统探索环境,生成一个从起始状态到终止状态的状态-动作-奖励序列,s1,a1,r1,.....,sT,aT,rT,在第 t 时刻,我们让 gt=rt+γrt+1+... 等于 q(st,a) ,从而求解策略梯度优化问题。
优化基本都是基于同策略的,也就是说每一步更新只会用最新的策略执行时采集到的数据。
策略优化通常还包括学习出![]() ,作为
,作为![]() 的近似,该函数用于确定如何更新策略。
的近似,该函数用于确定如何更新策略。
基于策略优化的方法举例:
2、Policy Gradient
Q-Learning和DQN都是基于价值的强化学习算法,在给定一个状态下,计算采取每个动作的价值,我们选择有最高Q值(在所有状态下最大的期望奖励)的行动。如果我们省略中间的步骤,即直接根据当前的状态来选择动作,也就引出了强化学习中的另一种很重要的算法,即策略梯度(Policy Gradient,PG)
策略梯度不通过误差反向传播,它通过观测信息选出一个行为直接进行反向传播,当然出人意料的是他并没有误差,而是利用reward奖励直接对选择行为的可能性进行增强和减弱,好的行为会被增加下一次被选中的概率,不好的行为会被减弱下次被选中的概率。
举例如下图所示:输入当前的状态,输出action的概率分布,选择概率最大的一个action作为要执行的操作。
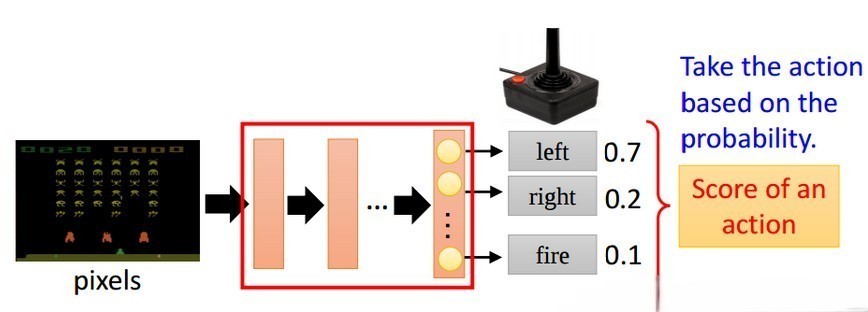
Policy Gradient算法的优缺点如下:
- 优点
- 连续的动作空间(或者高维空间)中更加高效;
- 可以实现随机化的策略;
- 某种情况下,价值函数可能比较难以计算,而策略函数较容易。
- 缺点
- 通常收敛到局部最优而非全局最优
- 评估一个策略通常低效(这个过程可能慢,但是具有更高的可变性,其中也会出现很多并不有效的尝试,而且方差高)
3、REINFORCE
蒙特卡罗策略梯度reinforce算法是策略梯度最简单的也是最经典的一个算法。
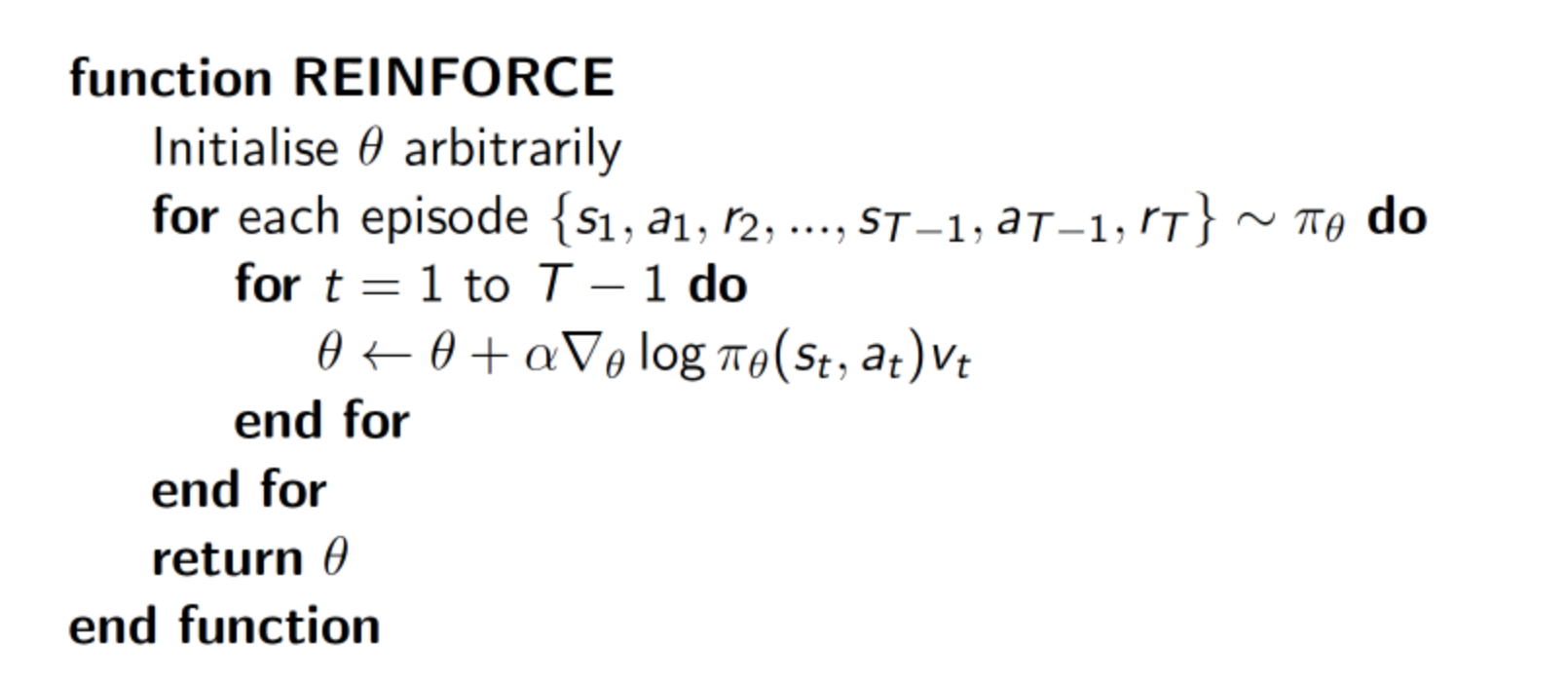
算法流程如下:
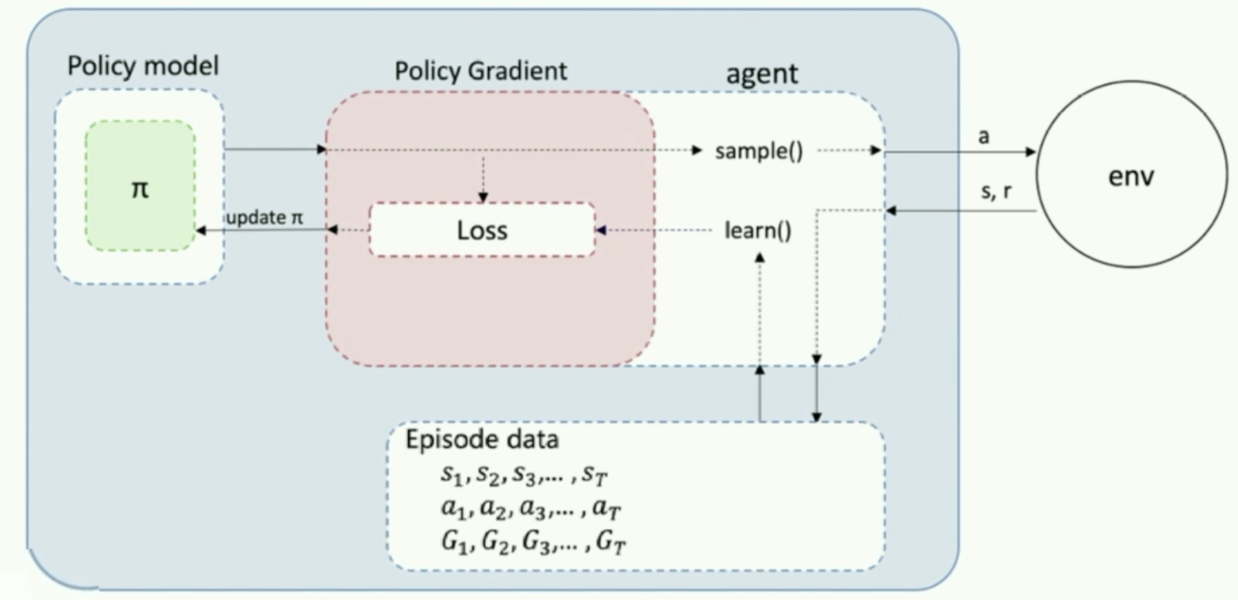
首先我们需要一个 policy model 来输出动作概率,输出动作概率后,我们 sample() 函数去得到一个具体的动作,然后跟环境交互过后,我们可以得到一整个回合的数据。拿到回合数据之后,我再去执行一下 learn() 函数,在 learn() 函数里面,我就可以拿这些数据去构造损失函数,然后扔给优化器去优化,去更新我的 policy model。
4、Actor Critic
演员-评论家算法(Actor-Critic)是基于策略(Policy Based)和基于价值(Value Based)相结合的方法
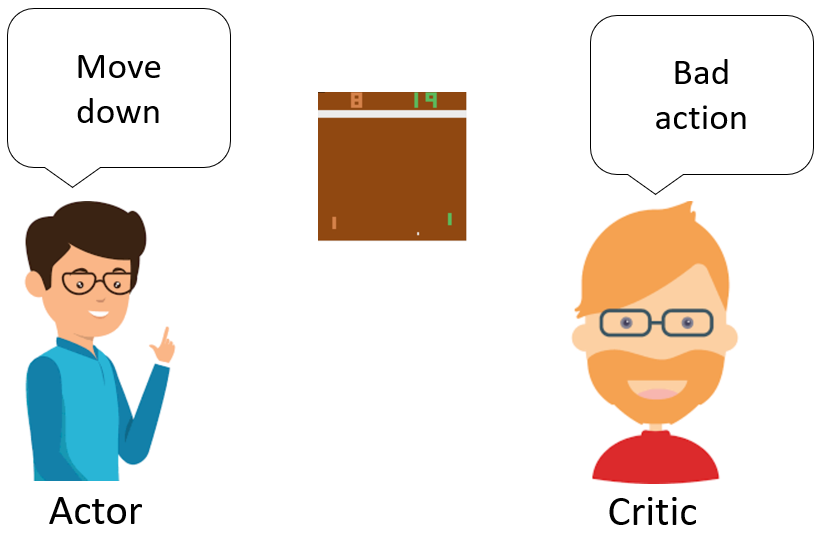
- 演员(Actor)是指策略函数πθ(a∣s),即学习一个策略来得到尽量高的回报。
- 评论家(Critic)是指值函数Vπ(s),对当前策略的值函数进行估计,即评估演员的好坏。
- 借助于价值函数,演员-评论家算法可以进行单步更新参数,不需要等到回合结束才进行更新。
Actor-Critic算法的网络结果如下:
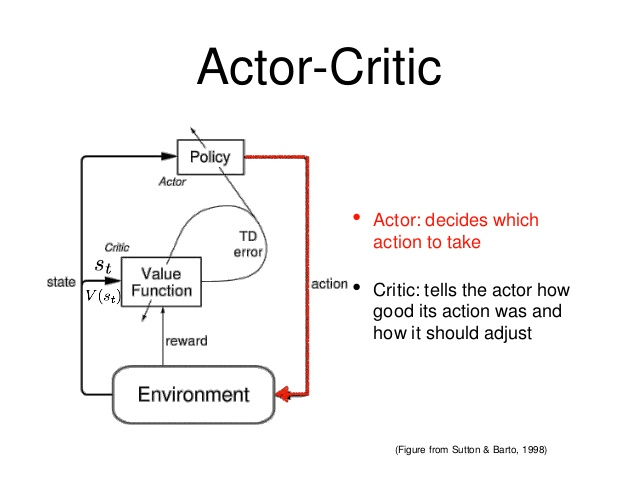
整体结构
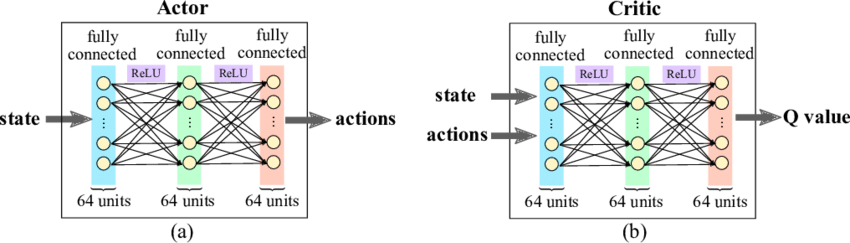
Actor和Critic的网络结构
Actor-Critic算法流程如下:

Actor-Critic算法也存在一些算法上的原生瓶颈:
- Actor Critic 取决于 Critic 的价值判断, 但是 Critic 难收敛, 再加上 Actor 的更新, 就更难收敛,为了解决该问题又提出了 A3C 算法和 DDPG 算法。
5、异步的优势行动者评论家算法(Asynchronous Advantage Actor-Critic,A3C)
相比Actor-Critic,A3C的优化主要有3点,分别是
- 异步训练框架
- 网络结构优化
- Critic评估点的优化
其中异步训练框架是最大的优化。
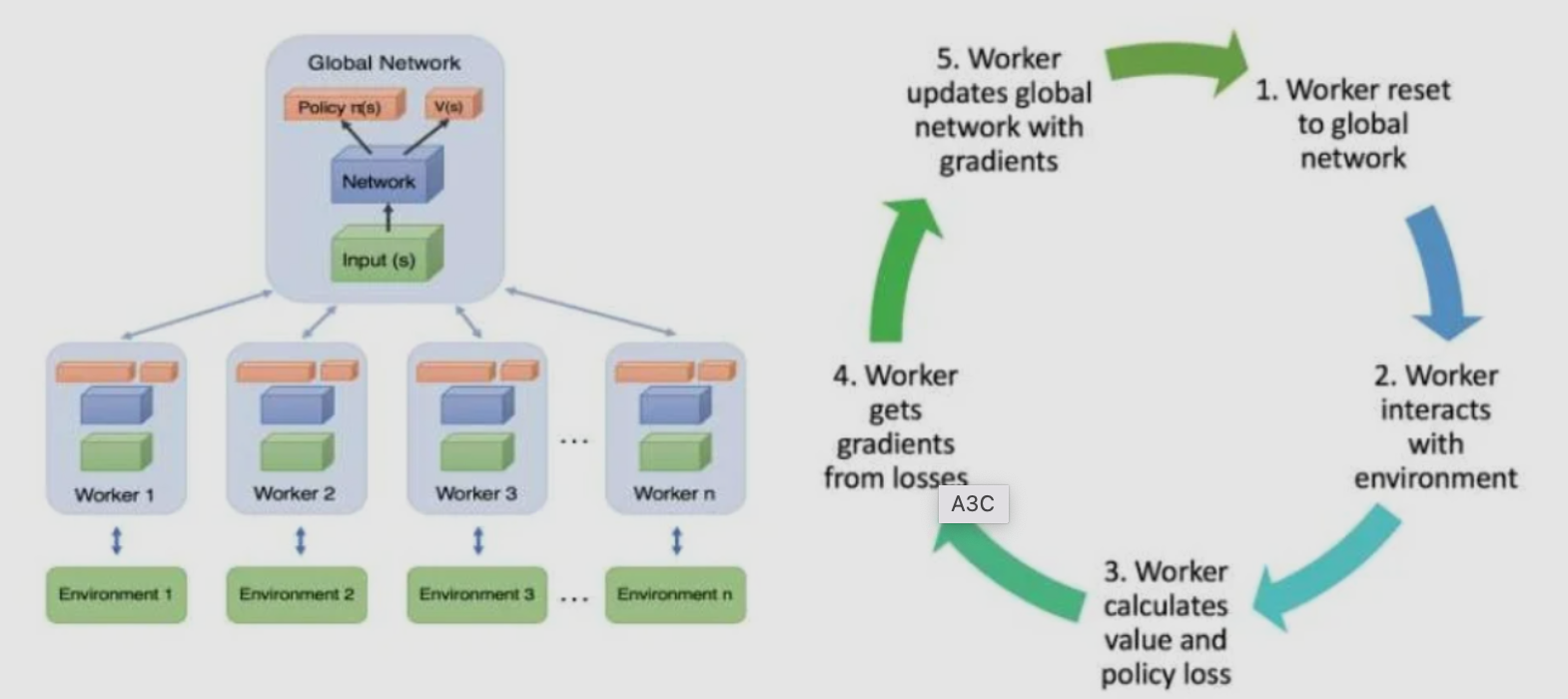
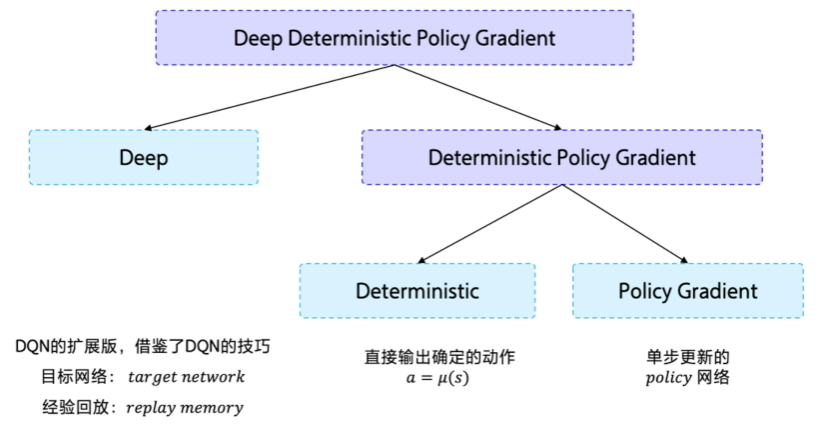
6、深度确定性策略梯度(Deep Deterministic Policy Gradient,DDPG)
从DDPG这个名字看,它是由D(Deep)+D(Deterministic )+ PG(Policy Gradient)组成。
- Deep 是因为用了神经网络;
- Deterministic 表示 DDPG 输出的是一个确定性的动作,可以用于连续动作的一个环境;
- Policy Gradient 代表的是它用到的是策略网络。REINFORCE 算法每隔一个 episode 就更新一次,但 DDPG 网络是每个 step 都会更新一次 policy 网络,也就是说它是一个单步更新的 policy 网络。
6、Q-Learning
Q-Learning是强化学习算法中value-based的算法,Q即为Q(s,a),就是在某一个时刻的state状态下,采取动作a能够获得未来收益的折现值,环境会根据agent的动作反馈相应的reward奖赏,所以算法的主要思想就是将state和action构建成一张Q_table表来存储Q值,然后根据Q值来选取能够获得最大收益的动作。我们不断的迭代我们的Q值表使其最终收敛,然后根据Q值表我们就可以在每个状态下选取一个最优策略。
这个系列的算法学习最优行动值函数![]() 的近似函数:
的近似函数:![]() 。Q存储了所有状态步(s)中对应动作(a)的概率。
。Q存储了所有状态步(s)中对应动作(a)的概率。
它们通常使用基于贝尔曼方程的目标函数。优化过程属于异策略系列,这意味着每次更新可以使用任意时间点的训练数据,不管获取数据时智能体选择如何探索环境。
- 智能体每一步的行动由该式子给出:
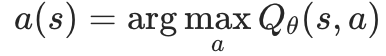
- 奖励由r表示,一般来说是任务成功时获得一次奖励
Q Learning 的算法框架是让系统按照策略指引进行探索,在探索每一步都进行状态价值的更新。其中最优行动值函数Q的更新算法如下:

其中,Q是递归定义的,
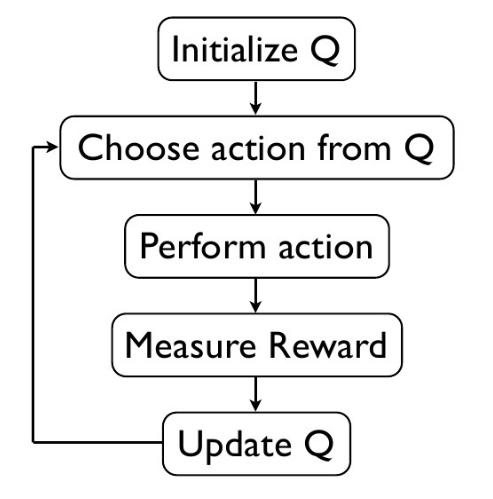
- Q(s1)的奖励来自于所有之后的步骤
- 离s1越远,奖励衰减的越厉害,也可以简单理解为离梯度源头越远,梯度传播的效果就越差

参数介绍:
- Epsilon greedy:是用在决策上的一个策略,比如epsilon = 0.9的时候,就说明百分之90的情况我会按照Q表的最优值选择行为,百分之10的时间随机选择行为。
- alpha:学习率,决定这次的误差有多少是要被学习的。
- gamma:对未来reward的衰减值。gamma越接近1,机器对未来的reward越敏感
基于 Q-Learning 的方法
- DQN:一个让深度强化学习得到发展的经典方法
- C51:学习关于回报的分布函数,其期望是
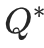
7、Deep Q Network(DQN)
在普通的Q-learning中,当状态和动作空间是离散且维数不高时可使用Q-Table储存每个状态动作对的Q值,而当状态和动作空间是高维连续时,使用Q-Table不现实,我们无法构建可以存储超大状态空间的Q_table。
为了解决超大状态空间Q-table的存储和提取问题,神经网络技术被引入了强化学习,可以将状态和动作当成神经网络的输入,然后经过神经网络分析后得到动作的 Q 值,这样就没必要在表格中记录 Q 值,而是直接使用神经网络预测Q值。同时也可以只输入状态输入神经网络,通过神经网络预测得到所有的动作,然后再根据价值选择策略函数选择出对应的动作。
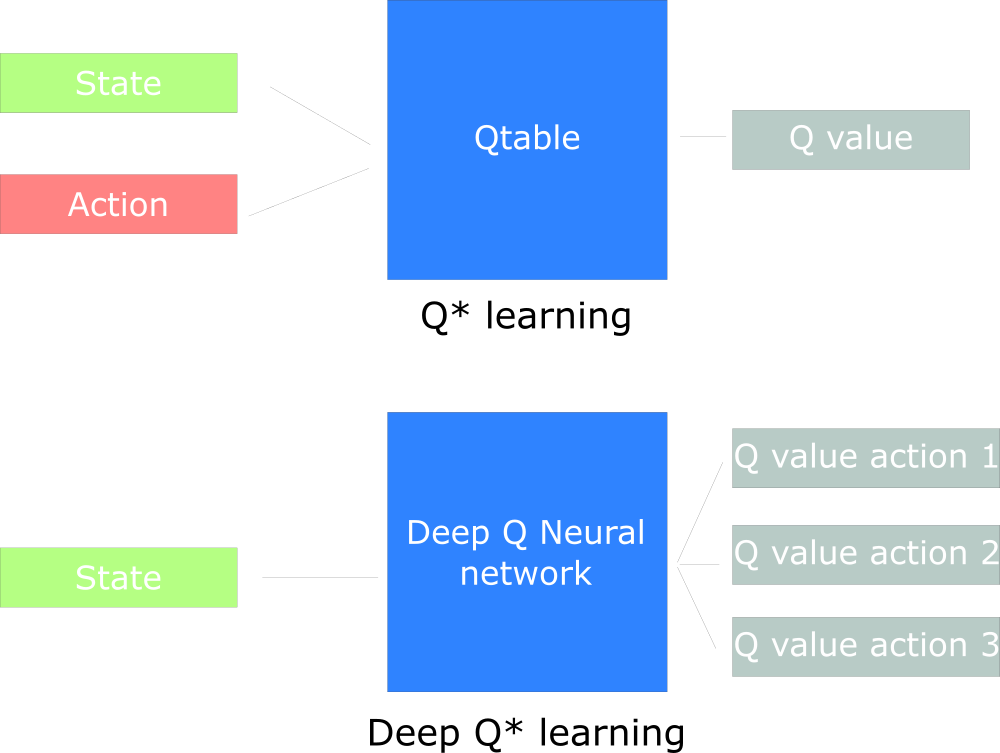
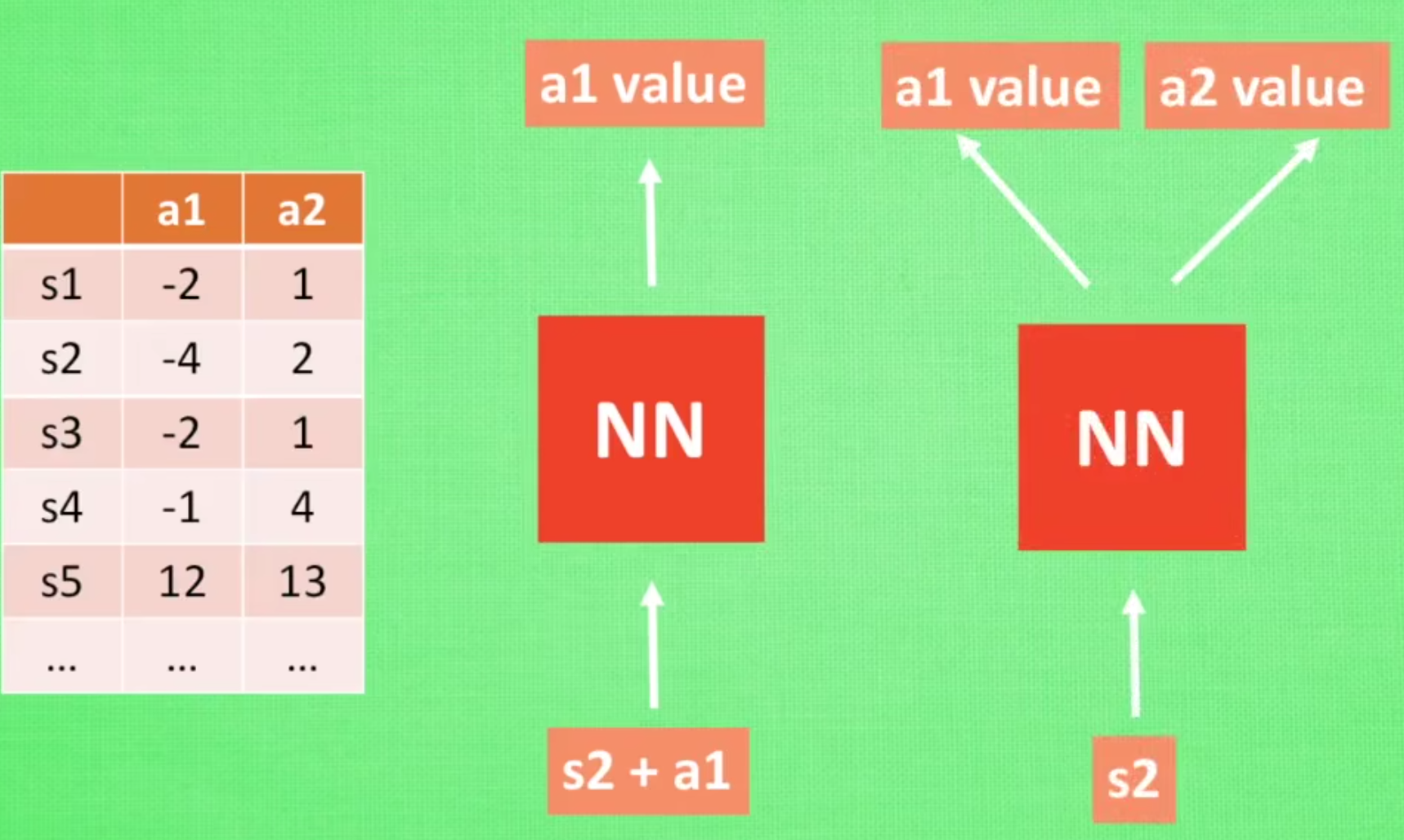
DQN的训练方式如下,
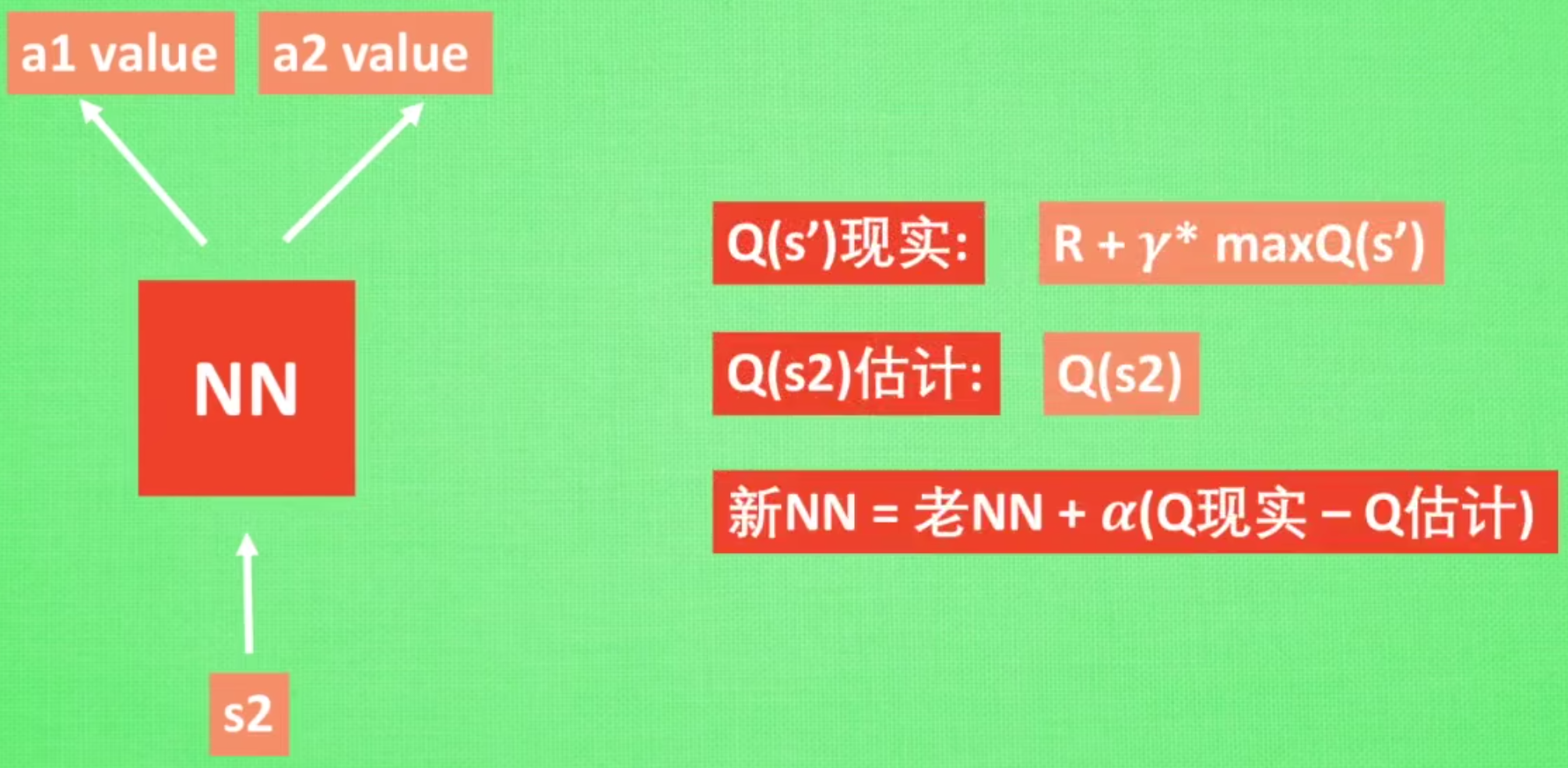
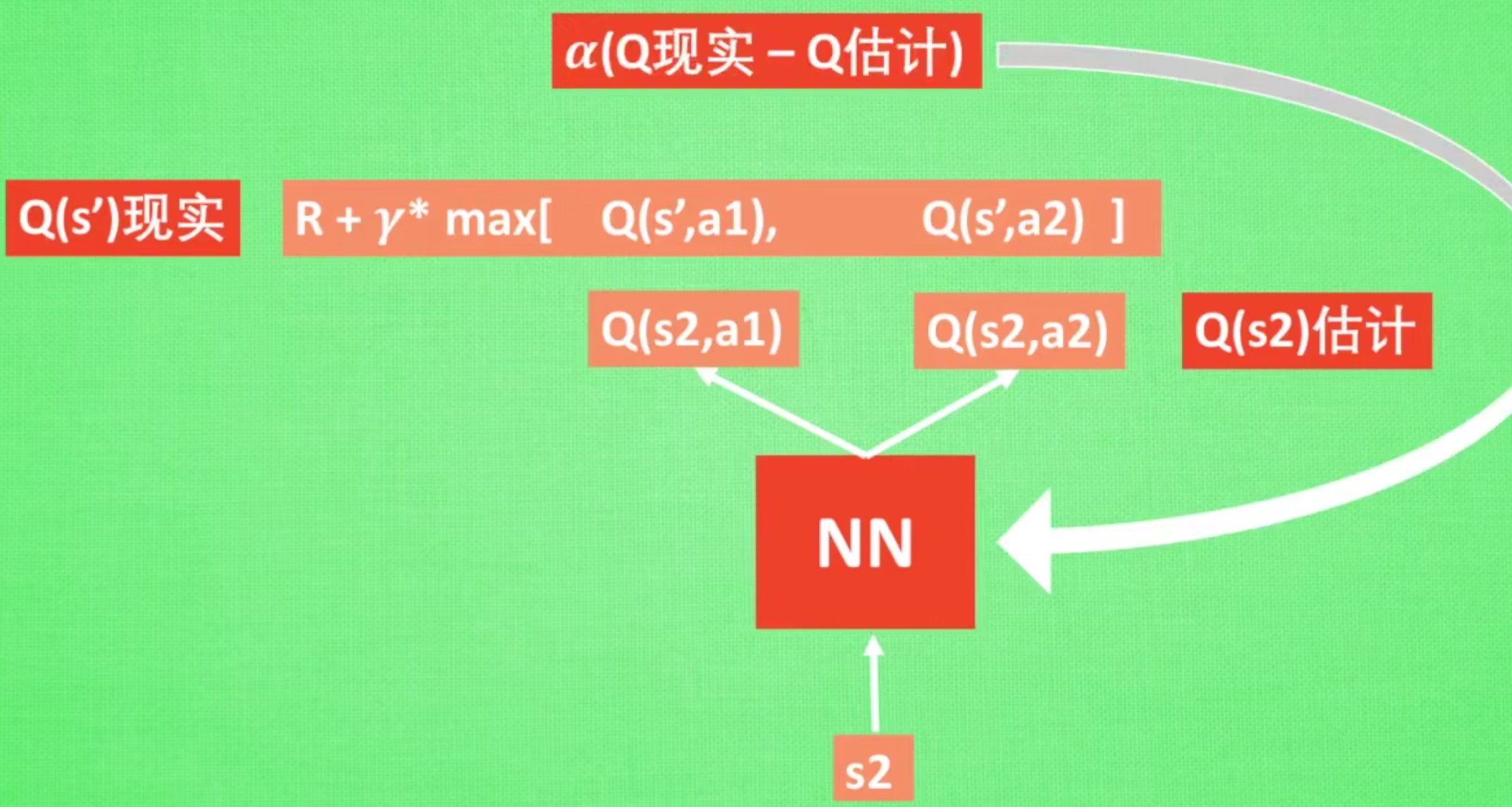
DQN相比Q-Learning,真正使它强大的原因有如下两点:
- 经验回放(experience replay):DQN利用Qlearning特点,目标策略与动作策略分离,学习时利用经验池储存的经验取batch更新Q。同时提高了样本的利用率,也打乱了样本状态相关性使其符合神经网络的使用特点。
- 固定Q目标(fixed Q-targets):神经网络一般学习的是固定的目标,而Qlearning中Q同样为学习的变化量,变动太大不利于学习。所以DQN使Q在一段时间内保持不变,使神经网络更易于学习。

整体算法流程如下,
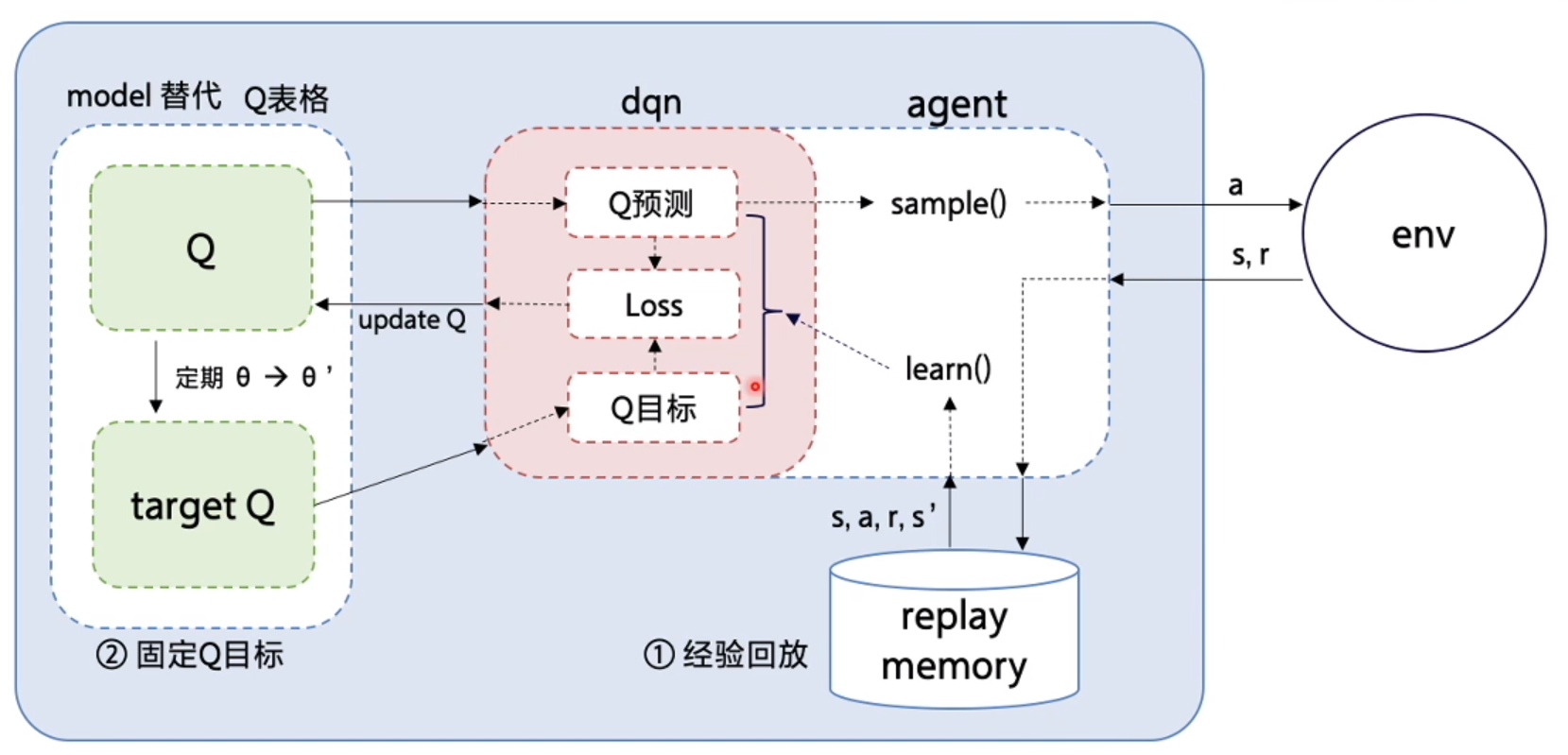
DQN也存在一些算法上的原生瓶颈:
- 在估计值函数的时候一个任意小的变化可能导致对应动作被选择或者不被选择,这种不连续的变化是致使基于值函数的方法无法得到收敛保证的重要因素。
- 选择最大的Q值这样一个搜索过程在高纬度或者连续空间是非常困难的;
- 无法学习到随机策略,有些情况下随机策略往往是最优策略。
8、Sarsa

0x2:有模型学习
1、纯规划
这种方法不采用显示地表示策略,而是纯使用规划技术来选择行动,例如 模型预测控制 (model-predictive control, MPC)。在模型预测控制中,智能体每次观察环境的时候,都会计算得到一个对于当前模型最优的规划,这里的规划指的是未来一个固定时间段内,智能体会采取的所有行动(通过学习值函数,规划算法可能会考虑到超出范围的未来奖励)。智能体先执行规划的第一个行动,然后立即舍弃规划的剩余部分。每次准备和环境进行互动时,它会计算出一个新的规划,从而避免执行小于规划范围的规划给出的行动。
- MBMF 在一些深度强化学习的标准基准任务上,基于学习到的环境模型进行模型预测控制
2、Expert Iteration
Expert Iteration是纯规划的后来之作,它使用、学习策略的显示表示形式:
![]()
智能体在模型中应用了一种规划算法,类似蒙特卡洛树搜索(Monte Carlo Tree Search),通过对当前策略进行采样生成规划的候选行为。这种算法得到的行动比策略本身生成的要好,所以相对于策略来说,它是“专家”。随后更新策略,以产生更类似于规划算法输出的行动。
参考链接:
https://easyai.tech/blog/introduction-to-reinforcement-learning/ https://imzhanghao.com/2022/02/10/reinforcement-learning/
0x1:Q-Learning案例
1、treasure_on_right -- 一个简单的命令行寻宝游戏

""" A simple example for Reinforcement Learning using table lookup Q-learning method. An agent "o" is on the left of a 1 dimensional world, the treasure is on the rightmost location. Run this program and to see how the agent will improve its strategy of finding the treasure. View more on my tutorial page: https://morvanzhou.github.io/tutorials/ """ import numpy as np import pandas as pd import time np.random.seed(2) # reproducible N_STATES = 32 # the length of the 1 dimensional world ACTIONS = ['left', 'right'] # available actions EPSILON = 0.9 # greedy police ALPHA = 0.1 # learning rate GAMMA = 0.9 # discount factor MAX_EPISODES = 999 # maximum episodes FRESH_TIME = 0.1 # fresh time for one move def build_q_table(n_states, actions): table = pd.DataFrame( np.zeros((n_states, len(actions))), # q_table initial values columns=actions, # actions's name ) # print(table) # show table return table def choose_action(state, q_table): # This is how to choose an action state_actions = q_table.iloc[state, :] if (np.random.uniform() > EPSILON) or ((state_actions == 0).all()): # act non-greedy or state-action have no value action_name = np.random.choice(ACTIONS) else: # act greedy action_name = state_actions.idxmax() # replace argmax to idxmax as argmax means a different function in newer version of pandas return action_name def get_env_feedback(S, A): # This is how agent will interact with the environment if A == 'right': # move right if S == N_STATES - 2: # terminate S_ = 'terminal' R = 1 else: S_ = S + 1 R = 0 else: # move left R = 0 if S == 0: S_ = S # reach the wall else: S_ = S - 1 return S_, R def update_env(S, episode, step_counter): # This is how environment be updated env_list = ['-']*(N_STATES-1) + ['T'] # '---------T' our environment if S == 'terminal': interaction = 'Episode %s: total_steps = %s' % (episode+1, step_counter) print('\r{}'.format(interaction), end='') time.sleep(2) print('\r ', end='') else: env_list[S] = 'o' interaction = ''.join(env_list) print('\r{}'.format(interaction), end='') time.sleep(FRESH_TIME) def rl(): # main part of RL loop q_table = build_q_table(N_STATES, ACTIONS) for episode in range(MAX_EPISODES): step_counter = 0 S = 0 is_terminated = False update_env(S, episode, step_counter) while not is_terminated: A = choose_action(S, q_table) S_, R = get_env_feedback(S, A) # take action & get next state and reward q_predict = q_table.loc[S, A] # q_predict: current action's action_probability if S_ != 'terminal': q_target = R + GAMMA * q_table.iloc[S_, :].max() # next state is not terminal else: q_target = R # next state is terminal is_terminated = True # terminate this episode q_table.loc[S, A] += ALPHA * (q_target - q_predict) # update the current action's action_probability, which make the currently selected action more likely to occur, S = S_ # move to next state update_env(S, episode, step_counter+1) step_counter += 1 print('\r\nQ-table: {0}\n'.format(q_table)) return q_table if __name__ == "__main__": q_table = rl() print('\r\nQ-table:\n') print(q_table)
View Code
每一步的qtable概率表如下:

Q-table: left right 0 0.0 0.0 1 0.0 0.0 2 0.0 0.0 3 0.0 0.0 4 0.0 0.1 5 0.0 0.0 Q-table: left right 0 0.0 0.000 1 0.0 0.000 2 0.0 0.000 3 0.0 0.009 4 0.0 0.190 5 0.0 0.000 Q-table: left right 0 0.0 0.00000 1 0.0 0.00000 2 0.0 0.00081 3 0.0 0.02520 4 0.0 0.27100 5 0.0 0.00000 Q-table: left right 0 0.0 0.000000 1 0.0 0.000073 2 0.0 0.002997 3 0.0 0.047070 4 0.0 0.343900 5 0.0 0.000000 Q-table: left right 0 0.00000 0.000007 1 0.00000 0.000572 2 0.00003 0.006934 3 0.00000 0.073314 4 0.00000 0.409510 5 0.00000 0.000000 Q-table: left right 0 0.00000 0.000057 1 0.00000 0.001138 2 0.00003 0.012839 3 0.00000 0.102839 4 0.00000 0.468559 5 0.00000 0.000000 Q-table: left right 0 0.00000 0.000154 1 0.00000 0.002180 2 0.00003 0.020810 3 0.00000 0.134725 4 0.00000 0.521703 5 0.00000 0.000000 Q-table: left right 0 0.00000 0.000335 1 0.00000 0.003835 2 0.00003 0.030854 3 0.00000 0.168206 4 0.00000 0.569533 5 0.00000 0.000000 Q-table: left right 0 0.00000 0.000647 1 0.00000 0.006228 2 0.00003 0.042907 3 0.00000 0.202643 4 0.00000 0.612580 5 0.00000 0.000000 Q-table: left right 0 0.00000 0.001142 1 0.00000 0.009467 2 0.00003 0.056855 3 0.00000 0.237511 4 0.00000 0.651322 5 0.00000 0.000000 Q-table: left right 0 0.00000 0.001880 1 0.00000 0.013637 2 0.00003 0.072545 3 0.00000 0.272379 4 0.00000 0.686189 5 0.00000 0.000000 Q-table: left right 0 0.000000 0.002920 1 0.000000 0.018803 2 0.000030 0.089805 3 0.000000 0.337965 4 0.027621 0.717570 5 0.000000 0.000000 Q-table: left right 0 0.000000 0.004320 1 0.000000 0.025005 2 0.000030 0.111241 3 0.000000 0.368750 4 0.027621 0.745813 5 0.000000 0.000000 Q-table: left right 0 0.000000 0.006138 1 0.000000 0.032516 2 0.000030 0.133304 3 0.000000 0.398998 4 0.027621 0.771232 5 0.000000 0.000000 Q-table: left right 0 0.000552 0.008451 1 0.000000 0.041262 2 0.000030 0.155884 3 0.000000 0.428509 4 0.027621 0.794109 5 0.000000 0.000000 Q-table: left right 0 0.000552 0.011319 1 0.000000 0.051165 2 0.000030 0.178861 3 0.000000 0.457128 4 0.027621 0.814698 5 0.000000 0.000000 Q-table: left right 0 0.000552 0.014792 1 0.000000 0.062146 2 0.000030 0.202117 3 0.000000 0.484738 4 0.027621 0.833228 5 0.000000 0.000000 Q-table: left right 0 0.000552 0.018906 1 0.000000 0.074122 2 0.000030 0.225531 3 0.000000 0.511255 4 0.027621 0.849905 5 0.000000 0.000000 Q-table: left right 0 0.000552 0.023687 1 0.000000 0.087008 2 0.000030 0.248991 3 0.000000 0.536621 4 0.027621 0.864915 5 0.000000 0.000000 Q-table: left right 0 0.000552 0.029149 1 0.000000 0.100716 2 0.000030 0.272388 3 0.000000 0.560801 4 0.027621 0.878423 5 0.000000 0.000000 Q-table: left right 0 0.000552 0.035298 1 0.000000 0.115159 2 0.000030 0.295621 3 0.000000 0.604459 4 0.077399 0.890581 5 0.000000 0.000000 Q-table: left right 0 0.000552 0.042133 1 0.000000 0.130249 2 0.000030 0.320461 3 0.000000 0.624166 4 0.077399 0.901523 5 0.000000 0.000000 Q-table: left right 0 0.000552 0.049642 1 0.000000 0.146066 2 0.000030 0.344589 3 0.000000 0.642886 4 0.077399 0.911371 5 0.000000 0.000000 Q-table: left right 0 0.000552 0.057824 1 0.000000 0.162472 2 0.000030 0.367990 3 0.000000 0.660621 4 0.077399 0.920234 5 0.000000 0.000000 Q-table: left right 0 0.000552 0.066664 1 0.000000 0.179344 2 0.000030 0.390647 3 0.000000 0.677380 4 0.077399 0.928210 5 0.000000 0.000000 Q-table: left right 0 0.000552 0.076138 1 0.000000 0.196568 2 0.000030 0.412547 3 0.000000 0.693181 4 0.077399 0.935389 5 0.000000 0.000000 Q-table: left right 0 0.000552 0.086216 1 0.000000 0.214040 2 0.000030 0.433678 3 0.000000 0.708048 4 0.077399 0.941850 5 0.000000 0.000000 Q-table: left right 0 0.000552 0.096858 1 0.000000 0.231667 2 0.000030 0.454035 3 0.000000 0.722009 4 0.077399 0.947665 5 0.000000 0.000000 Q-table: left right 0 0.000552 0.108022 1 0.000000 0.249364 2 0.000030 0.473612 3 0.000000 0.735098 4 0.077399 0.952899 5 0.000000 0.000000 Q-table: left right 0 0.000552 0.119663 1 0.000000 0.267053 2 0.000030 0.492410 3 0.000000 0.747349 4 0.077399 0.957609 5 0.000000 0.000000 Q-table: left right 0 0.000552 0.131731 1 0.000000 0.284664 2 0.000030 0.510430 3 0.000000 0.769104 4 0.137951 0.961848 5 0.000000 0.000000 Episode 32: total_steps = 5
View Code
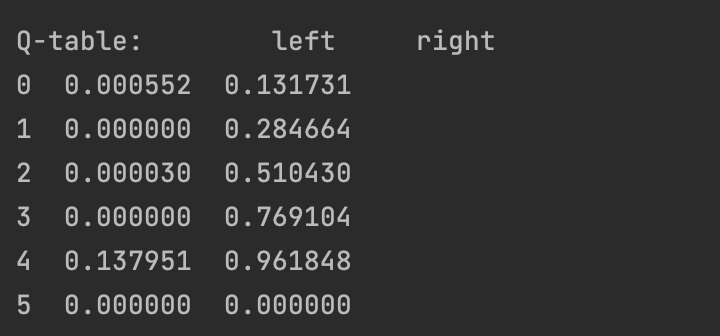
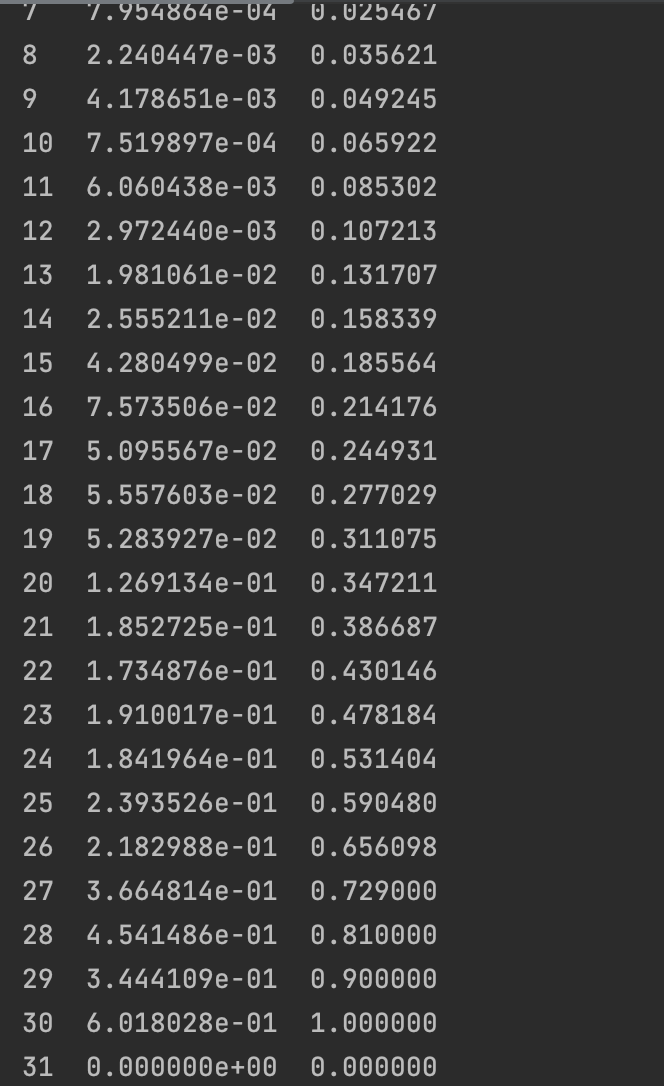
经过了几十轮次的迭代后,Q-table基本收敛完成了,此时right概率的平均概率就超过了EPSILON*left,此时可以认为算法已经学会了一种大概率获胜的行动策略。
为了更好地理解这个算法,我们逐步分析Q-table的值变化过程,以 N_STATES=8 为例。
- Q-table初始化
Q-table: left right 0 0.0 0.0 1 0.0 0.0 2 0.0 0.0 3 0.0 0.0 4 0.0 0.0 5 0.0 0.0 6 0.0 0.0 7 0.0 0.0
- episode_1循环
由于整个Q-table所有的 (s,a) 都为零,所以agent在探索过程中,q_target,q_predict都为零,此时不存在Q-table更新动作。
只有当小圆点经过一定步骤的随机运动,刚好运气好到达终点时,才能获得一个R=1的奖励,此时可以理解为算法获得了第一个梯度。
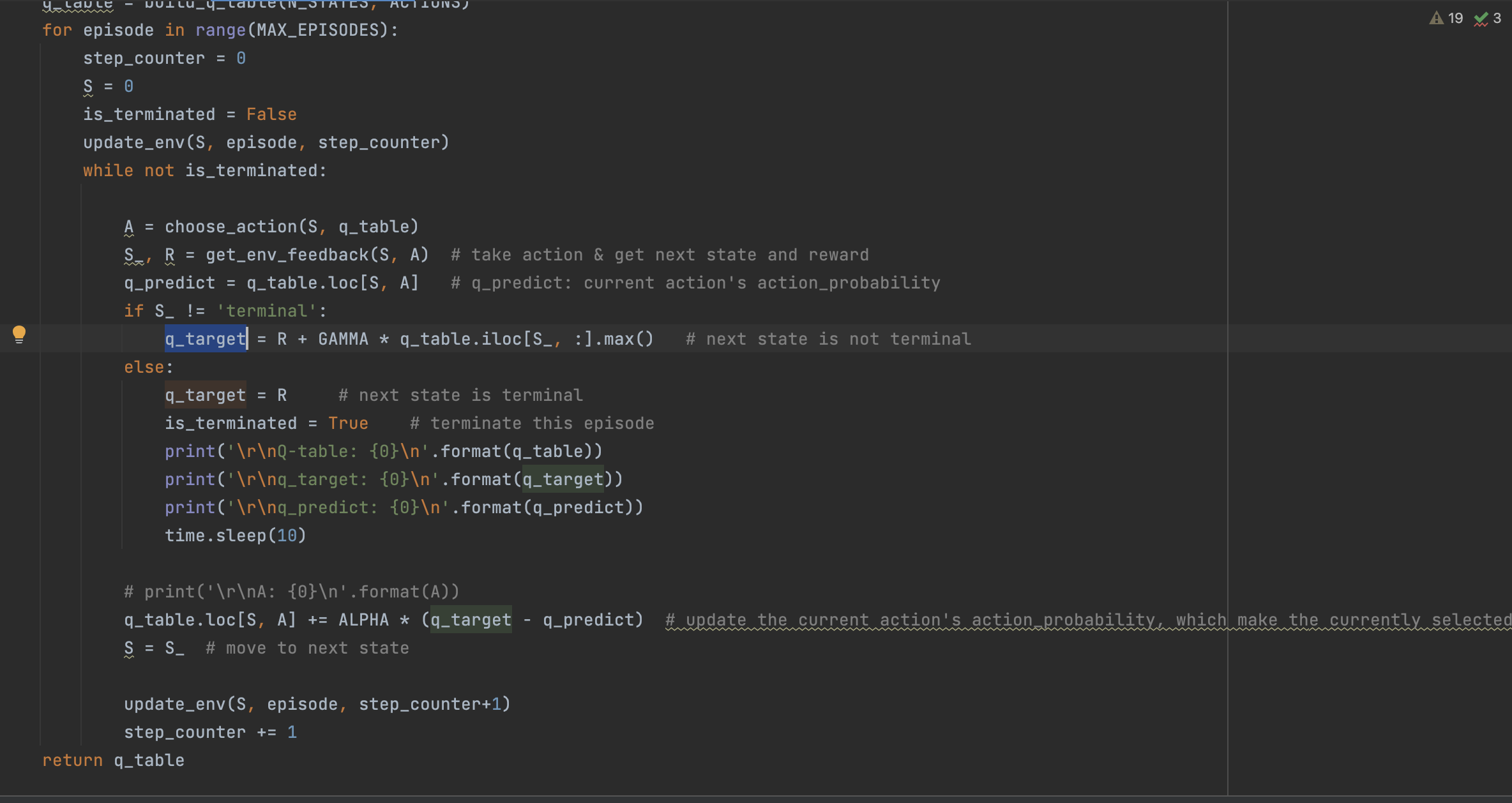
此时 q_target=1;q_predict=0,所以 ALPHA * (q_target - q_predict) = 0.1,且只有 (S=6,A=right) 能获得这次Q-table概率更新。
注意!这是Q-table的第一次概率更新,这个概率更新的根源是”目标达到的R奖励“,而 (S=6,A=right) 是引导算法获得这次奖励的行动路径。后续的所有概率更新都是从这里开始的。
更新后的Q-table如下:
Q-table: left right 0 0.0 0.000 1 0.0 0.000 2 0.0 0.000 3 0.0 0.000 4 0.0 0.000 5 0.0 0.000 6 0.0 0.100 7 0.0 0.000
- episode_2循环
此时,整个Q-table,除了S=6,其他的 (s,a) 依然都为零,所以小圆点在 S=5 之前不管如何做随机运动,都不会发生概率更新动作。
有趣地”分水岭“发生在 S=5 的时候,在 S=5 这个点,由于此时 (S=5,a)依然都为零,所以小圆点依然是在做随机运动,
- 随机向left的运动,由于 S=4 的 (s,a) 为零,所以不会产生概率更新,小圆点运动到 S=4 之后,要通过随机运动”碰运气“再次来到 S=5,才能再次来到这个”分水岭“
- 随机向right的运动,由于 S=6 的 (s,a) 不为零,所以这里会产生概率更新,q_target = R + GAMMA * q_table.iloc[6, :].max() = 0.09;q_predict=0;ALPHA * (q_target - q_predict) = 0.09
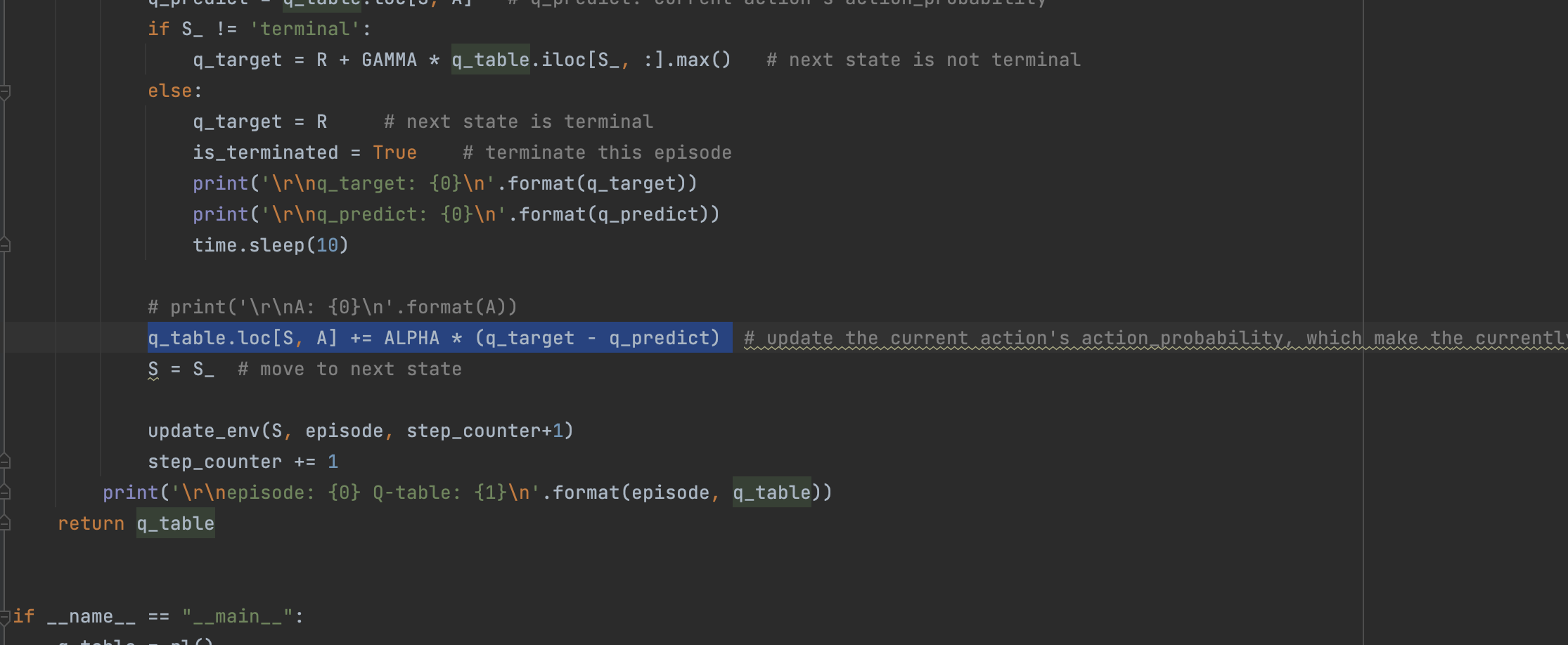
计算得到 (S=5, A=right) = 0.09。
更新后的Q-table如下:
0 0.0 0.000 1 0.0 0.000 2 0.0 0.000 3 0.0 0.000 4 0.0 0.000 5 0.0 0.009 6 0.0 0.100 7 0.0 0.000
接下来S+1,继续更新S=6的动作概率。
在 S=6这个状态上,
- (S=6,left)=0
- (S=6,right)=0,1
所以根据最大概率决策(本例中Epsilon=0.9,即90%时候按照最大概率,10%时候引入随机扰动),小圆点选择向right方向运动。注意!这里算法允许一定概率的随机扰动,即不按照最大概率方向选择action动作。

S=6向right运动到达终点,所以此时q_target=R=1
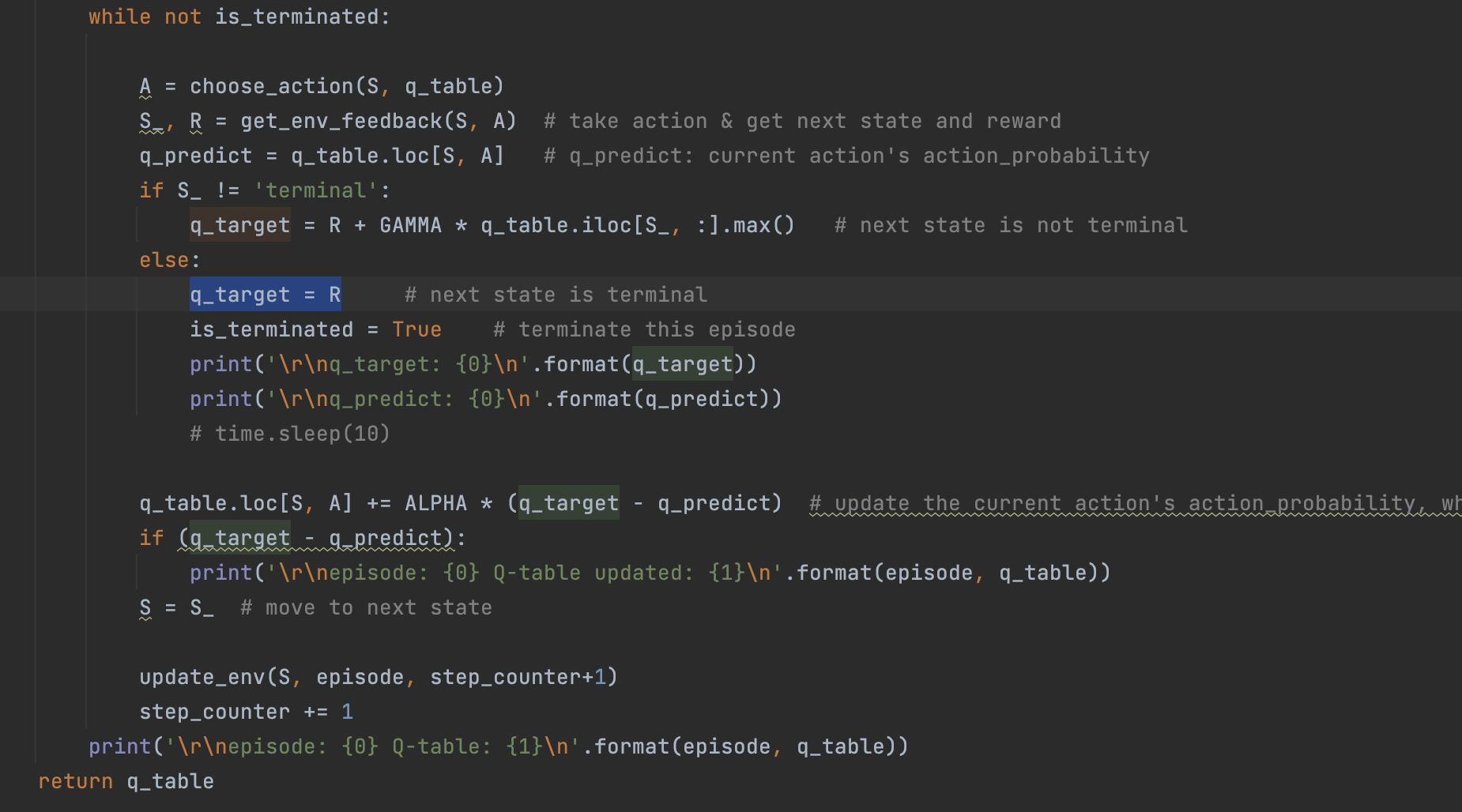
所以有q_predict = q_table.loc[6, A] = 0.1;ALPHA * (q_target - q_predict) = 0.09;
所以有q_table.loc[6, right] += ALPHA * (q_target - q_predict) = 0.1+0.09 = 0.19;
更新后的Q-table如下:
0 0.0 0.000 1 0.0 0.000 2 0.0 0.000 3 0.0 0.000 4 0.0 0.000 5 0.0 0.009 6 0.0 0.190 7 0.0 0.000
- episode_3循环
和前面的分析过程类似,”分水岭“发生在 S=4 的时候,在 S=4 这个点,由于此时 (S=4,a)依然都为零,所以小圆点依然是在做随机运动,
- 随机向left的运动,由于 S=3 的 (s,a) 为零,所以不会产生概率更新,小圆点运动到 S=4 之后,要通过随机运动”碰运气“再次来到 S=5,才能再次来到这个”分水岭“
- 随机向right的运动,由于 S=5 的 (s,a) 不为零,所以这里会产生概率更新,q_target = R + GAMMA * q_table.iloc[5, :].max() = 0.00081;q_predict=0;ALPHA * (q_target - q_predict) = 0.00081
计算得到 (S=4, A=right) = 0.09。
更新后的Q-table如下:
0 0.0 0.00000 1 0.0 0.00000 2 0.0 0.00000 3 0.0 0.00000 4 0.0 0.00081 5 0.0 0.00900 6 0.0 0.19000 7 0.0 0.00000
S=5的更新逻辑和S=4类似,S=6的更新逻辑和前面分析的也类似。
- episode_N循环
按照同样的漏记,不断循环,最终算法逐渐收敛,
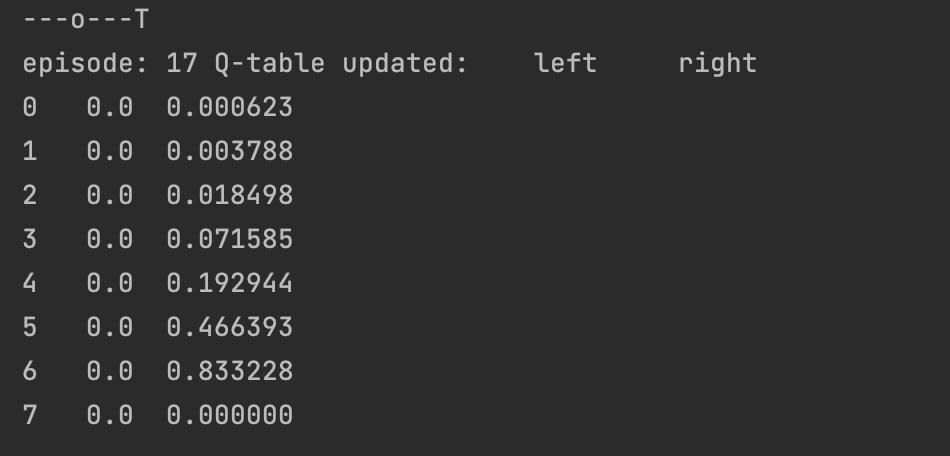
至此,我们可以总结一下Q-learn算法思想:
- 算法的初始化从随机或者全零开始,第一次迭代完全依靠随机运动,也就是依靠”运气“去完成第一次任务。所以如果搜索空间过大,则算法的冷启动可能会是一个问题。
- 算法的第一次任务完成获得一次奖励R,这个奖励R是整个优化过程的”第一推动力“,起到了类似”梯度“的作用,后续的整个优化都是基于这个”梯度“不断往前传播优化的。
- 每一步S的动作选择,都是基于当前Q-table中该S的最优概率进行决策的,这个特征保证了整个算法的最终收敛性。
- 算法在每一步S,在选择了最优动作Action后,会对下一步动作的概率进行”展望“,其本质是在进行一种概率评估。从本质结果上看,这一步的作用是向更高概率的 (S,A)方向,提高对应 (S, A) 概率,这是一种概率梯度模仿策略。因为整个迭代过程的首个梯度是倒数最后一步正确动作获得的奖励,所以原则上,整个优化过程会朝着最终完成任务的方向进行优化。
2、机器人走迷宫游戏
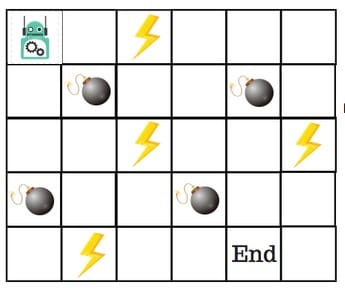
假设机器人必须越过迷宫并到达终点。有地雷,机器人一次只能移动一个地砖。如果机器人踏上矿井,机器人就死了。机器人必须在尽可能短的时间内到达终点。
得分/奖励系统如下:
- 机器人在每一步都失去1点。这样做是为了使机器人采用最短路径并尽可能快地到达目标。
- 如果机器人踩到地雷,则点损失为100并且游戏结束。
- 如果机器人获得动力⚡️,它会获得1点。
- 如果机器人达到最终目标,则机器人获得100分。
现在,显而易见的问题是:
我们如何训练机器人以最短的路径到达最终目标而不踩矿井?
Q值表(Q-Table)是一个简单查找表的名称,我们计算每个状态的最大预期未来奖励。基本上,这张表将指导我们在每个状态采取最佳行动。
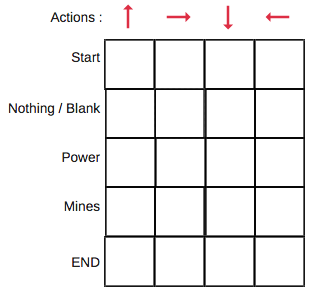
Q函数(Q-Function)即为上文提到的动作价值函数,他有两个输入:「状态」和「动作」。它将返回在该状态下执行该动作的未来奖励期望。
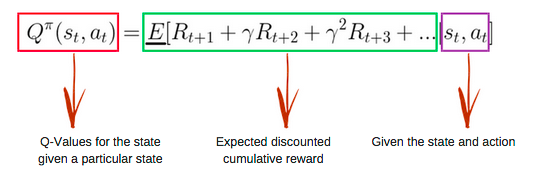
我们可以把Q函数视为一个在Q-Table上滚动的读取器,用于寻找与当前状态关联的行以及与动作关联的列。它会从相匹配的单元格中返回 Q 值。这就是未来奖励的期望。

在我们探索环境(environment)之前,Q-table 会给出相同的任意的设定值(大多数情况下是 0)。随着对环境的持续探索,这个 Q-table 会通过迭代地使用 Bellman 方程(动态规划方程)更新 Q(s,a) 来给出越来越好的近似。
下面来逐步分析算法优化过程,
- 第1步:初始化Q值表
我们将首先构建一个Q值表。有n列,其中n=操作数。有m行,其中m=状态数。我们将值初始化为0
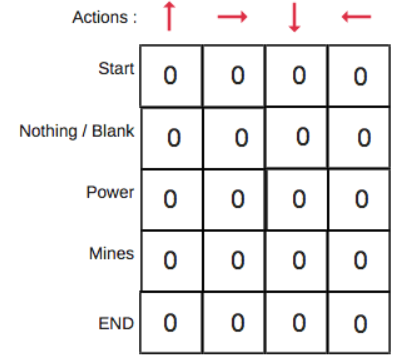
- 步骤2和3:选择并执行操作
这些步骤的组合在不确定的时间内完成。这意味着此步骤一直运行,直到我们停止训练,或者训练循环停止。
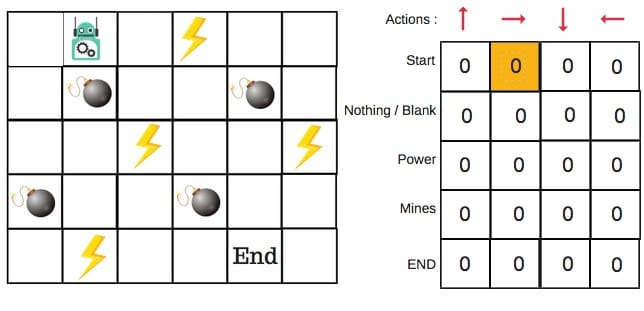
如果每个Q值都等于零,我们就需要权衡探索/利用(exploration/exploitation)的程度了,思路就是,在一开始,我们将使用 epsilon 贪婪策略:
- 我们指定一个探索速率「epsilon」,一开始将它设定为 1。这个就是我们将随机采用的步长。在一开始,这个速率应该处于最大值,因为我们不知道 Q-table 中任何的值。这意味着,我们需要通过随机选择动作进行大量的探索。
- 生成一个随机数。如果这个数大于 epsilon,那么我们将会进行「利用」(这意味着我们在每一步利用已经知道的信息选择动作)。否则,我们将继续进行探索。
- 在刚开始训练 Q 函数时,我们必须有一个大的 epsilon(即刚开始需要更多的随机探索)。随着智能体对估算出的 Q 值更有把握,我们将逐渐减小 epsilon(到了中后期按照历史经验可以更好地行动)。
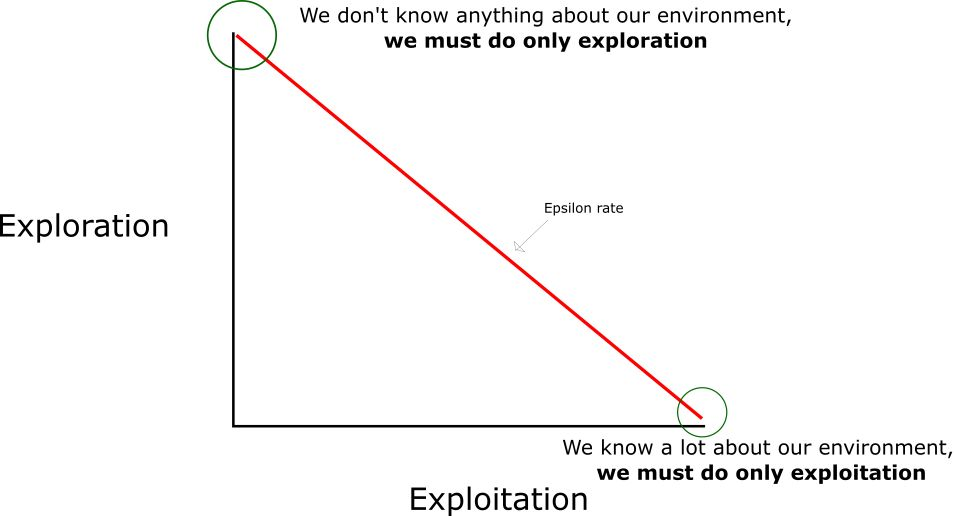
- 步骤4和5:评估
现在我们采取了行动并观察了结果和奖励。我们需要更新功能Q(s,a):
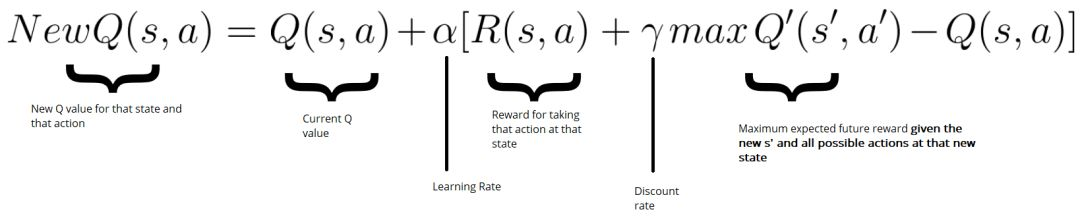
最后生成的Q表:
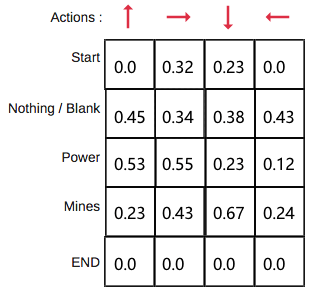
3、maze -- 一个简单的跳方格游戏
run_this.py

""" Reinforcement learning maze example. Red rectangle: explorer. Black rectangles: hells [reward = -1]. Yellow bin circle: paradise [reward = +1]. All other states: ground [reward = 0]. This script is the main part which controls the update method of this example. The RL is in RL_brain.py. View more on my tutorial page: https://morvanzhou.github.io/tutorials/ """ from maze_env import Maze from RL_brain import QLearningTable def update(): for episode in range(100): # initial observation observation = env.reset() print("observation: ", observation) print("str(observation): ", str(observation)) while True: # fresh env env.render() # RL choose action based on observation action = RL.choose_action(str(observation)) # RL take action and get next observation and reward observation_, reward, done = env.step(action) # RL learn from this transition RL.learn(str(observation), action, reward, str(observation_)) # swap observation observation = observation_ # break while loop when end of this episode if done: break # end of game print('game over') env.destroy() if __name__ == "__main__": env = Maze() print("env.n_actions: ", env.n_actions) print("list(range(env.n_actions)): ", list(range(env.n_actions))) RL = QLearningTable(actions=list(range(env.n_actions))) env.after(100, update) env.mainloop()
View Code
maze_env.py

""" Reinforcement learning maze example. Red rectangle: explorer. Black rectangles: hells [reward = -1]. Yellow bin circle: paradise [reward = +1]. All other states: ground [reward = 0]. This script is the environment part of this example. The RL is in RL_brain.py. View more on my tutorial page: https://morvanzhou.github.io/tutorials/ """ import random import numpy as np import time import sys if sys.version_info.major == 2: import Tkinter as tk else: import tkinter as tk UNIT = 40 # pixels MAZE_H = 16 # grid height MAZE_W = 16 # grid width class Maze(tk.Tk, object): def __init__(self): super(Maze, self).__init__() self.action_space = ['u', 'd', 'l', 'r'] self.n_actions = len(self.action_space) self.title('maze') self.geometry('{0}x{1}'.format(MAZE_W * UNIT, MAZE_H * UNIT)) self._build_maze() def _build_maze(self): self.canvas = tk.Canvas(self, bg='white', height=MAZE_H * UNIT, width=MAZE_W * UNIT) # create grids for c in range(0, MAZE_W * UNIT, UNIT): x0, y0, x1, y1 = c, 0, c, MAZE_H * UNIT self.canvas.create_line(x0, y0, x1, y1) for r in range(0, MAZE_H * UNIT, UNIT): x0, y0, x1, y1 = 0, r, MAZE_W * UNIT, r self.canvas.create_line(x0, y0, x1, y1) # create origin #origin = np.array([random.randint(UNIT, UNIT*MAZE_W), random.randint(UNIT, UNIT*MAZE_W)]) origin = np.array([20+(UNIT)*random.randint(1, 3), 20+(UNIT)*random.randint(1, 3)]) # hell hell1_center = origin + np.array([UNIT * 2, UNIT]) self.hell1 = self.canvas.create_rectangle( hell1_center[0] - 15, hell1_center[1] - 15, hell1_center[0] + 15, hell1_center[1] + 15, fill='black') # hell hell2_center = origin + np.array([UNIT, UNIT * 2]) self.hell2 = self.canvas.create_rectangle( hell2_center[0] - 15, hell2_center[1] - 15, hell2_center[0] + 15, hell2_center[1] + 15, fill='black') # create oval oval_center = origin + UNIT * 2 self.oval = self.canvas.create_oval( oval_center[0] - 15, oval_center[1] - 15, oval_center[0] + 15, oval_center[1] + 15, fill='yellow') # create red rect self.rect = self.canvas.create_rectangle( origin[0] - 15, origin[1] - 15, origin[0] + 15, origin[1] + 15, fill='red') # pack all self.canvas.pack() def reset(self): self.update() time.sleep(0.5) self.canvas.delete(self.rect) origin = np.array([20, 20]) self.rect = self.canvas.create_rectangle( origin[0] - 15, origin[1] - 15, origin[0] + 15, origin[1] + 15, fill='red') # return observation return self.canvas.coords(self.rect) def step(self, action): s = self.canvas.coords(self.rect) base_action = np.array([0, 0]) if action == 0: # up if s[1] > UNIT: base_action[1] -= UNIT elif action == 1: # down if s[1] < (MAZE_H - 1) * UNIT: base_action[1] += UNIT elif action == 2: # right if s[0] < (MAZE_W - 1) * UNIT: base_action[0] += UNIT elif action == 3: # left if s[0] > UNIT: base_action[0] -= UNIT self.canvas.move(self.rect, base_action[0], base_action[1]) # move agent s_ = self.canvas.coords(self.rect) # next state # reward function if s_ == self.canvas.coords(self.oval): reward = 1 done = True s_ = 'terminal' elif s_ in [self.canvas.coords(self.hell1), self.canvas.coords(self.hell2)]: reward = -1 done = True s_ = 'terminal' else: reward = 0 done = False return s_, reward, done def render(self): time.sleep(0.1) self.update() def update(): for t in range(10): s = env.reset() while True: env.render() a = 1 s, r, done = env.step(a) if done: break if __name__ == '__main__': env = Maze() env.after(100, update) env.mainloop()
View Code
RL_brain.py

""" This part of code is the Q learning brain, which is a brain of the agent. All decisions are made in here. View more on my tutorial page: https://morvanzhou.github.io/tutorials/ """ import numpy as np import pandas as pd class QLearningTable: def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9): self.actions = actions # a list self.lr = learning_rate self.gamma = reward_decay self.epsilon = e_greedy self.q_table = pd.DataFrame(columns=self.actions, dtype=np.float64) def choose_action(self, observation): self.check_state_exist(observation) # action selection if np.random.uniform() < self.epsilon: # choose best action state_action = self.q_table.loc[observation, :] # some actions may have the same value, randomly choose on in these actions action = np.random.choice(state_action[state_action == np.max(state_action)].index) else: # choose random action action = np.random.choice(self.actions) return action def learn(self, s, a, r, s_): self.check_state_exist(s_) q_predict = self.q_table.loc[s, a] if s_ != 'terminal': q_target = r + self.gamma * self.q_table.loc[s_, :].max() # next state is not terminal else: q_target = r # next state is terminal print("self.q_table: ", self.q_table) self.q_table.loc[s, a] += self.lr * (q_target - q_predict) # update def check_state_exist(self, state): if state not in self.q_table.index: # append new state to q table self.q_table = pd.concat([self.q_table, pd.DataFrame([pd.Series( [0]*len(self.actions), index=self.q_table.columns, name=state, )])])
View Code
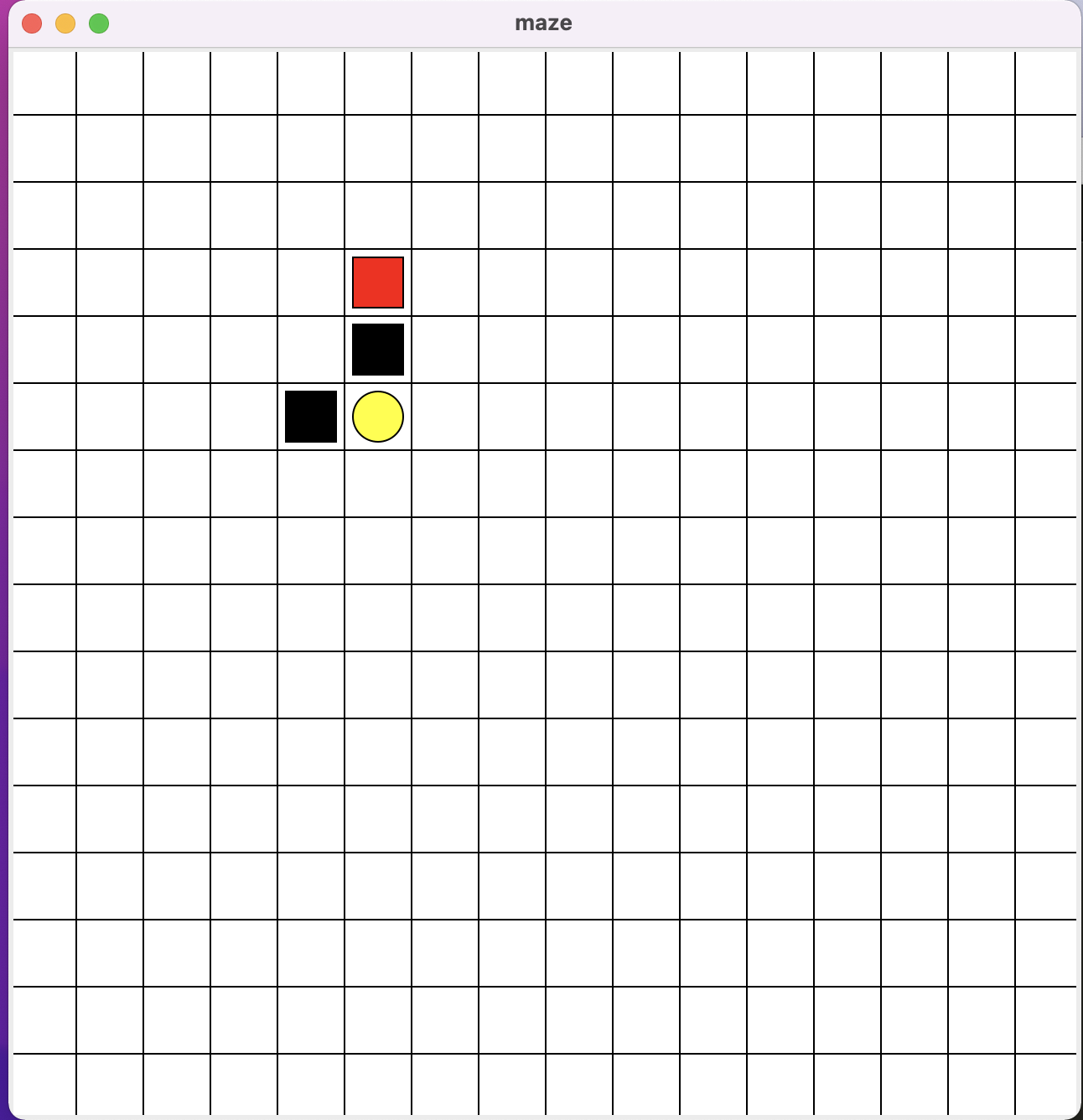
相比第一个命令行小游戏,该实验有几个值得注意的点:
- action动作空间有up、down、left、right四个方向
- state空间是整个画布上的所有坐标点
- Q-table是动态增长的,其实也可以在初始化的时候就按照画布大小给所有坐标点state进行初始化,但该实验想展示的点是一种更一般化的情况,虽然状态空间代表了完整地世界图景,但在大多数情况下,我们能实际观测到的状态是有限的,我们只能通过不断地尝试逐步丰富我们的状态空间
贝尔曼方程的误差传递和优化过程和第一个实验都是一样的。
0x2:Gym openai案例

import gymnasium as gym env = gym.make("LunarLander-v2", render_mode="human") observation, info = env.reset(seed=42) for _ in range(2000): action = env.action_space.sample() # this is where you would insert your policy observation, reward, terminated, truncated, info = env.step(action) if terminated or truncated: observation, info = env.reset() env.close()
View Code
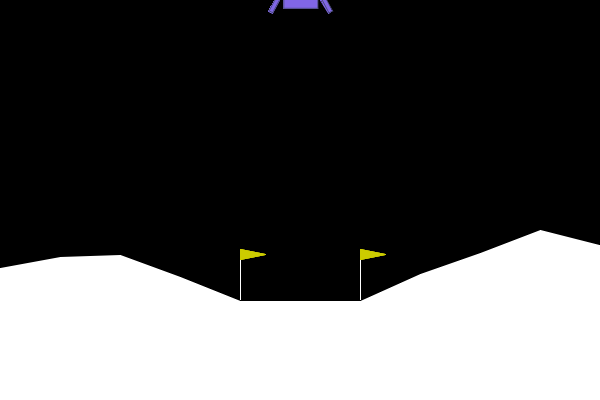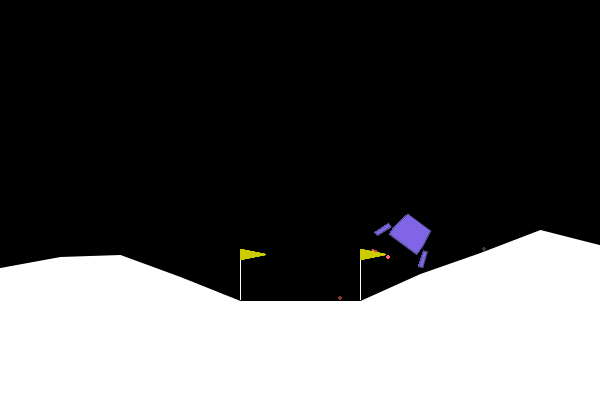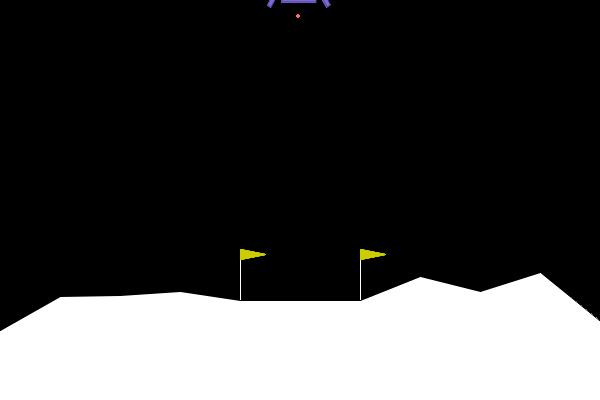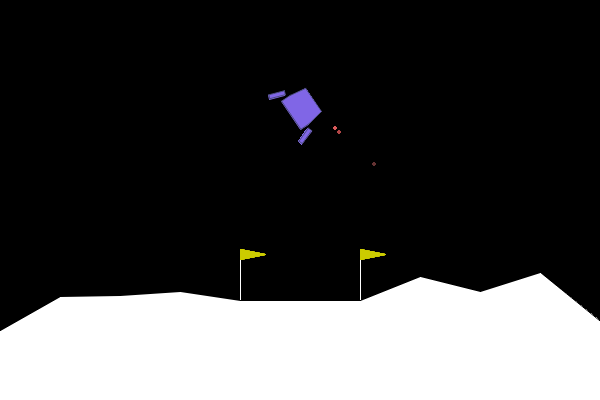
0x3:Sarsa案例
1、maze -- 一个简单的跳方格游戏
run_this.py

""" Sarsa is a online updating method for Reinforcement learning. Unlike Q learning which is a offline updating method, Sarsa is updating while in the current trajectory. You will see the sarsa is more coward when punishment is close because it cares about all behaviours, while q learning is more brave because it only cares about maximum behaviour. """ from maze_env import Maze from RL_brain import SarsaTable def update(): for episode in range(100): # initial observation observation = env.reset() # RL choose action based on observation action = RL.choose_action(str(observation)) while True: # fresh env env.render() # RL take action and get next observation and reward observation_, reward, done = env.step(action) # RL choose action based on next observation action_ = RL.choose_action(str(observation_)) # RL learn from this transition (s, a, r, s, a) ==> Sarsa RL.learn(str(observation), action, reward, str(observation_), action_) # swap observation and action observation = observation_ action = action_ # break while loop when end of this episode if done: print("RL.q_table: ", RL.q_table) break # end of game print('game over') env.destroy() if __name__ == "__main__": env = Maze() RL = SarsaTable(actions=list(range(env.n_actions))) env.after(100, update) env.mainloop()
View Code
maze_env.py

""" Reinforcement learning maze example. Red rectangle: explorer. Black rectangles: hells [reward = -1]. Yellow bin circle: paradise [reward = +1]. All other states: ground [reward = 0]. This script is the environment part of this example. The RL is in RL_brain.py. View more on my tutorial page: https://morvanzhou.github.io/tutorials/ """ import random import numpy as np import time import sys if sys.version_info.major == 2: import Tkinter as tk else: import tkinter as tk UNIT = 40 # pixels MAZE_H = 4 # grid height MAZE_W = 4 # grid width class Maze(tk.Tk, object): def __init__(self): super(Maze, self).__init__() self.action_space = ['u', 'd', 'l', 'r'] self.n_actions = len(self.action_space) self.title('maze') self.geometry('{0}x{1}'.format(MAZE_W * UNIT, MAZE_H * UNIT)) self._build_maze() def _build_maze(self): self.canvas = tk.Canvas(self, bg='white', height=MAZE_H * UNIT, width=MAZE_W * UNIT) # create grids for c in range(0, MAZE_W * UNIT, UNIT): x0, y0, x1, y1 = c, 0, c, MAZE_H * UNIT self.canvas.create_line(x0, y0, x1, y1) for r in range(0, MAZE_H * UNIT, UNIT): x0, y0, x1, y1 = 0, r, MAZE_W * UNIT, r self.canvas.create_line(x0, y0, x1, y1) # create origin origin = np.array([20, 20]) #origin = np.array([20 + (UNIT) * random.randint(1, 3), 20 + (UNIT) * random.randint(1, 3)]) # hell hell1_center = origin + np.array([UNIT * 2, UNIT]) self.hell1 = self.canvas.create_rectangle( hell1_center[0] - 15, hell1_center[1] - 15, hell1_center[0] + 15, hell1_center[1] + 15, fill='black') # hell hell2_center = origin + np.array([UNIT, UNIT * 2]) self.hell2 = self.canvas.create_rectangle( hell2_center[0] - 15, hell2_center[1] - 15, hell2_center[0] + 15, hell2_center[1] + 15, fill='black') # create oval oval_center = origin + UNIT * 2 self.oval = self.canvas.create_oval( oval_center[0] - 15, oval_center[1] - 15, oval_center[0] + 15, oval_center[1] + 15, fill='yellow') # create red rect self.rect = self.canvas.create_rectangle( origin[0] - 15, origin[1] - 15, origin[0] + 15, origin[1] + 15, fill='red') # pack all self.canvas.pack() def reset(self): self.update() time.sleep(0.5) self.canvas.delete(self.rect) origin = np.array([20, 20]) self.rect = self.canvas.create_rectangle( origin[0] - 15, origin[1] - 15, origin[0] + 15, origin[1] + 15, fill='red') # return observation return self.canvas.coords(self.rect) def step(self, action): s = self.canvas.coords(self.rect) base_action = np.array([0, 0]) if action == 0: # up if s[1] > UNIT: base_action[1] -= UNIT elif action == 1: # down if s[1] < (MAZE_H - 1) * UNIT: base_action[1] += UNIT elif action == 2: # right if s[0] < (MAZE_W - 1) * UNIT: base_action[0] += UNIT elif action == 3: # left if s[0] > UNIT: base_action[0] -= UNIT self.canvas.move(self.rect, base_action[0], base_action[1]) # move agent s_ = self.canvas.coords(self.rect) # next state # reward function if s_ == self.canvas.coords(self.oval): reward = 1 done = True s_ = 'terminal' elif s_ in [self.canvas.coords(self.hell1), self.canvas.coords(self.hell2)]: reward = -1 done = True s_ = 'terminal' else: reward = 0 done = False return s_, reward, done def render(self): time.sleep(0.1) self.update()
View Code
RL_brain.py

""" This part of code is the Q learning brain, which is a brain of the agent. All decisions are made in here. View more on my tutorial page: https://morvanzhou.github.io/tutorials/ """ import numpy as np import pandas as pd class RL(object): def __init__(self, action_space, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9): self.actions = action_space # a list self.lr = learning_rate self.gamma = reward_decay self.epsilon = e_greedy self.q_table = pd.DataFrame(columns=self.actions, dtype=np.float64) def check_state_exist(self, state): if state not in self.q_table.index: # append new state to q table self.q_table = pd.concat([self.q_table, pd.DataFrame([pd.Series( [0] * len(self.actions), index=self.q_table.columns, name=state, )])]) def choose_action(self, observation): self.check_state_exist(observation) # action selection if np.random.rand() < self.epsilon: # choose best action state_action = self.q_table.loc[observation, :] # some actions may have the same value, randomly choose on in these actions action = np.random.choice(state_action[state_action == np.max(state_action)].index) else: # choose random action action = np.random.choice(self.actions) return action def learn(self, *args): pass # off-policy class QLearningTable(RL): def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9): super(QLearningTable, self).__init__(actions, learning_rate, reward_decay, e_greedy) def learn(self, s, a, r, s_): self.check_state_exist(s_) q_predict = self.q_table.loc[s, a] if s_ != 'terminal': q_target = r + self.gamma * self.q_table.loc[s_, :].max() # next state is not terminal else: q_target = r # next state is terminal self.q_table.loc[s, a] += self.lr * (q_target - q_predict) # update # on-policy class SarsaTable(RL): def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9): super(SarsaTable, self).__init__(actions, learning_rate, reward_decay, e_greedy) def learn(self, s, a, r, s_, a_): self.check_state_exist(s_) q_predict = self.q_table.loc[s, a] if s_ != 'terminal': q_target = r + self.gamma * self.q_table.loc[s_, a_] # next state is not terminal else: q_target = r # next state is terminal self.q_table.loc[s, a] += self.lr * (q_target - q_predict) # update
View Code
用和前面例子同样的跳方格游戏,我们来对比一下Q-learning和Sarsa算法的主要区别:
- Sarsa在每一步展望未来的值函数Q(s',a')时,不是选择S=s’中的max_action value,而是按照当前实际选择的(S=s‘,A=a’)选择实际对应的value,并用实际对应的Q'值对当前S的Q值进行更新。
- Sarsa算法相比于Q-learning可以更快地向任务目标收敛,所做的牺牲就是随机探索性变差了。
- Sarsa不再进行未来展望,而是一五一十根据策略函数选取未来动作,并计算“当前状态-动作”和“未来状态-动作”的价值差,来不断进行价值梯度更新,使得每一步状态S的动作价值都朝向最终完成任务的方向靠近。
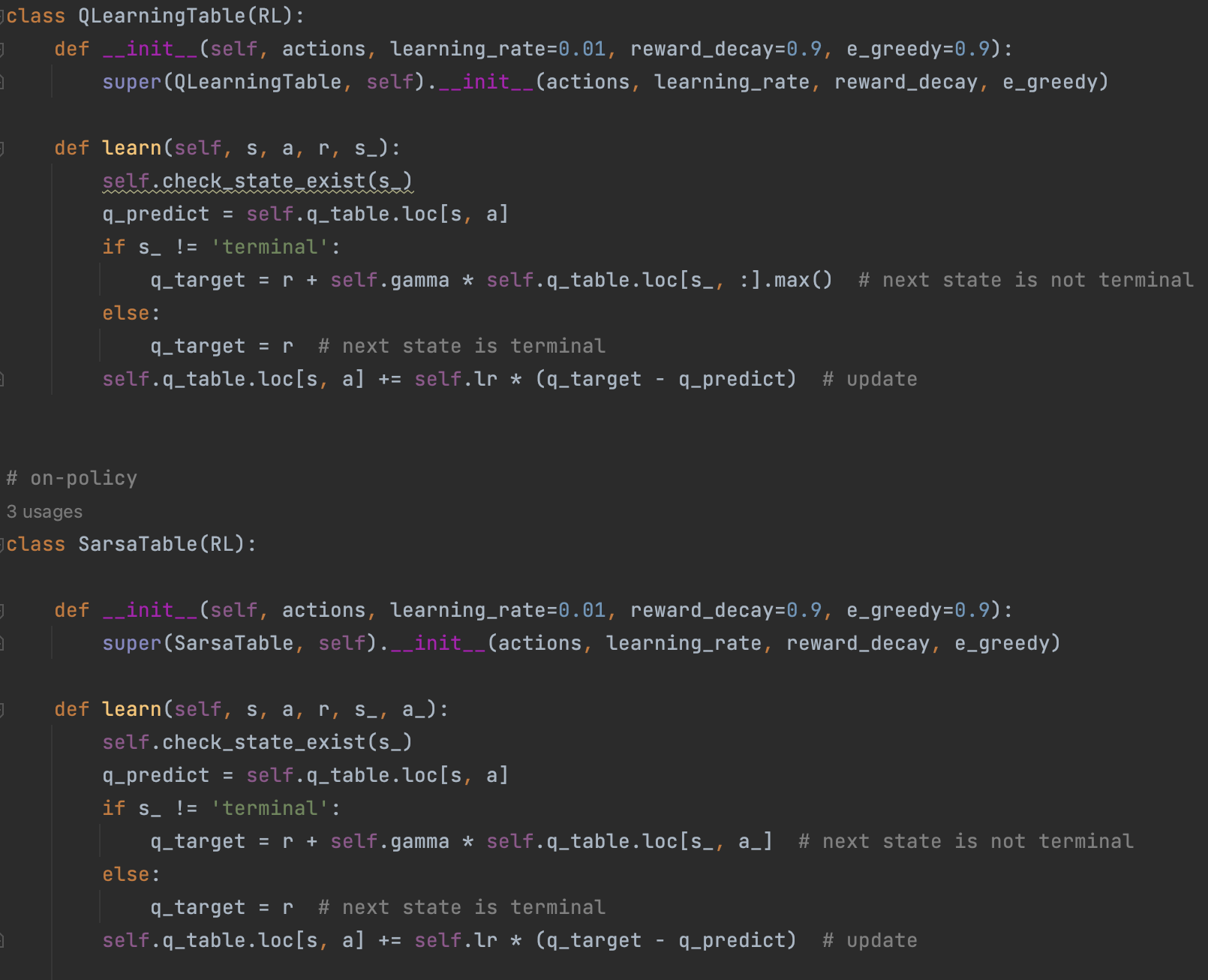
这种策略背后隐含的算法思想是:
每一步都脚踏实地,更多依靠已知的历史的经验和认知做出决策,当做出下一步决策后,不对未来展望抱过多的幻想,而是依然根据历史经验理性评估下一步决策能对最终目标带来的价值提升。按照这种稳妥地策略不断循环迭代,最终拟合出一个近似的全局最优行动策略。
2、Sarsa(λ) - 回合更新Q-table
run_this.py

""" Sarsa is a online updating method for Reinforcement learning. Unlike Q learning which is a offline updating method, Sarsa is updating while in the current trajectory. You will see the sarsa is more coward when punishment is close because it cares about all behaviours, while q learning is more brave because it only cares about maximum behaviour. """ from maze_env import Maze from RL_brain import SarsaLambdaTable def update(): for episode in range(100): # initial observation observation = env.reset() print("RL.q_table: ", RL.q_table) print("observation: ", observation) # RL choose action based on observation action = RL.choose_action(str(observation)) print("action = RL.choose_action(str(observation)) RL.q_table: ", RL.q_table) # initial all zero eligibility trace RL.eligibility_trace *= 0 while True: # fresh env env.render() # RL take action and get next observation and reward observation_, reward, done = env.step(action) # RL choose action based on next observation action_ = RL.choose_action(str(observation_)) # RL learn from this transition (s, a, r, s, a) ==> Sarsa RL.learn(str(observation), action, reward, str(observation_), action_) # swap observation and action observation = observation_ action = action_ # break while loop when end of this episode if done: print("RL.q_table: ", RL.q_table) break # end of game print('game over') env.destroy() if __name__ == "__main__": env = Maze() RL = SarsaLambdaTable(actions=list(range(env.n_actions))) env.after(100, update) env.mainloop()
View Code
maze_env.py

""" Reinforcement learning maze example. Red rectangle: explorer. Black rectangles: hells [reward = -1]. Yellow bin circle: paradise [reward = +1]. All other states: ground [reward = 0]. This script is the environment part of this example. The RL is in RL_brain.py. View more on my tutorial page: https://morvanzhou.github.io/tutorials/ """ import numpy as np import time import sys if sys.version_info.major == 2: import Tkinter as tk else: import tkinter as tk UNIT = 40 # pixels MAZE_H = 16 # grid height MAZE_W = 16 # grid width class Maze(tk.Tk, object): def __init__(self): super(Maze, self).__init__() self.action_space = ['u', 'd', 'l', 'r'] self.n_actions = len(self.action_space) self.title('maze') self.geometry('{0}x{1}'.format(MAZE_W * UNIT, MAZE_H * UNIT)) self._build_maze() def _build_maze(self): self.canvas = tk.Canvas(self, bg='white', height=MAZE_H * UNIT, width=MAZE_W * UNIT) # create grids for c in range(0, MAZE_W * UNIT, UNIT): x0, y0, x1, y1 = c, 0, c, MAZE_H * UNIT self.canvas.create_line(x0, y0, x1, y1) for r in range(0, MAZE_H * UNIT, UNIT): x0, y0, x1, y1 = 0, r, MAZE_W * UNIT, r self.canvas.create_line(x0, y0, x1, y1) # create origin origin = np.array([20+40*2, 20+40*2]) # hell hell1_center = origin + np.array([UNIT * 2, UNIT]) self.hell1 = self.canvas.create_rectangle( hell1_center[0] - 15, hell1_center[1] - 15, hell1_center[0] + 15, hell1_center[1] + 15, fill='black') # hell hell2_center = origin + np.array([UNIT, UNIT * 2]) self.hell2 = self.canvas.create_rectangle( hell2_center[0] - 15, hell2_center[1] - 15, hell2_center[0] + 15, hell2_center[1] + 15, fill='black') # create oval oval_center = origin + UNIT * 2 self.oval = self.canvas.create_oval( oval_center[0] - 15, oval_center[1] - 15, oval_center[0] + 15, oval_center[1] + 15, fill='yellow') # create red rect self.rect = self.canvas.create_rectangle( origin[0] - 15, origin[1] - 15, origin[0] + 15, origin[1] + 15, fill='red') # pack all self.canvas.pack() def reset(self): self.update() time.sleep(0.5) self.canvas.delete(self.rect) origin = np.array([20, 20]) self.rect = self.canvas.create_rectangle( origin[0] - 15, origin[1] - 15, origin[0] + 15, origin[1] + 15, fill='red') # return observation return self.canvas.coords(self.rect) def step(self, action): s = self.canvas.coords(self.rect) base_action = np.array([0, 0]) if action == 0: # up if s[1] > UNIT: base_action[1] -= UNIT elif action == 1: # down if s[1] < (MAZE_H - 1) * UNIT: base_action[1] += UNIT elif action == 2: # right if s[0] < (MAZE_W - 1) * UNIT: base_action[0] += UNIT elif action == 3: # left if s[0] > UNIT: base_action[0] -= UNIT self.canvas.move(self.rect, base_action[0], base_action[1]) # move agent s_ = self.canvas.coords(self.rect) # next state # reward function if s_ == self.canvas.coords(self.oval): reward = 1 done = True s_ = 'terminal' elif s_ in [self.canvas.coords(self.hell1), self.canvas.coords(self.hell2)]: reward = -1 done = True s_ = 'terminal' else: reward = 0 done = False return s_, reward, done def render(self): time.sleep(0.05) self.update()
View Code
RL_brain.py

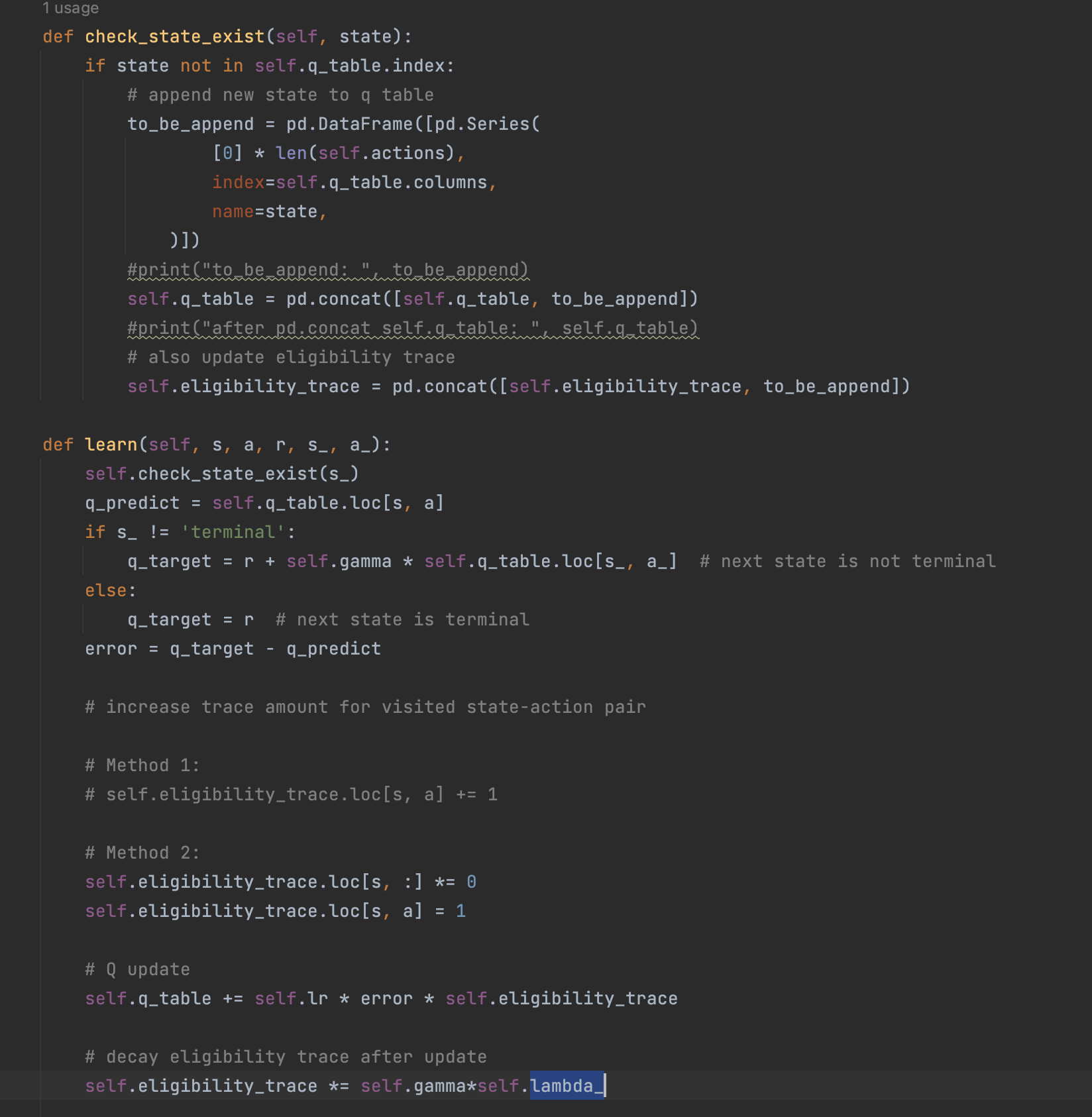
""" This part of code is the Q learning brain, which is a brain of the agent. All decisions are made in here. View more on my tutorial page: https://morvanzhou.github.io/tutorials/ """ import numpy as np import pandas as pd class RL(object): def __init__(self, action_space, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9): self.actions = action_space # a list self.lr = learning_rate self.gamma = reward_decay self.epsilon = e_greedy self.q_table = pd.DataFrame(columns=self.actions, dtype=np.float64) def check_state_exist(self, state): if state not in self.q_table.index: # append new state to q table self.q_table = pd.concat([self.q_table, pd.DataFrame([pd.Series( [0] * len(self.actions), index=self.q_table.columns, name=state, )])]) def choose_action(self, observation): self.check_state_exist(observation) # action selection if np.random.rand() < self.epsilon: # choose best action state_action = self.q_table.loc[observation, :] # some actions may have the same value, randomly choose on in these actions action = np.random.choice(state_action[state_action == np.max(state_action)].index) else: # choose random action action = np.random.choice(self.actions) return action def learn(self, *args): pass # backward eligibility traces class SarsaLambdaTable(RL): def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9, trace_decay=0.9): super(SarsaLambdaTable, self).__init__(actions, learning_rate, reward_decay, e_greedy) # backward view, eligibility trace. self.lambda_ = trace_decay self.eligibility_trace = self.q_table.copy() def check_state_exist(self, state): if state not in self.q_table.index: # append new state to q table to_be_append = pd.DataFrame([pd.Series( [0] * len(self.actions), index=self.q_table.columns, name=state, )]) #print("to_be_append: ", to_be_append) self.q_table = pd.concat([self.q_table, to_be_append]) #print("after pd.concat self.q_table: ", self.q_table) # also update eligibility trace self.eligibility_trace = pd.concat([self.eligibility_trace, to_be_append]) def learn(self, s, a, r, s_, a_): self.check_state_exist(s_) q_predict = self.q_table.loc[s, a] if s_ != 'terminal': q_target = r + self.gamma * self.q_table.loc[s_, a_] # next state is not terminal else: q_target = r # next state is terminal error = q_target - q_predict # increase trace amount for visited state-action pair # Method 1: # self.eligibility_trace.loc[s, a] += 1 # Method 2: self.eligibility_trace.loc[s, :] *= 0 self.eligibility_trace.loc[s, a] = 0.5 # Q update self.q_table += self.lr * error * self.eligibility_trace # decay eligibility trace after update self.eligibility_trace *= self.gamma*self.lambda_
View Code
Sarsa(λ)的算法流程如下:

用和前面例子同样的跳方格游戏,我们来对比一下Sarsa(λ)和Sarsa算法的主要区别:
- 奖励更新机制不同:
- Sarsa中,当进行奖励梯度传递的时候,Q-table每次只更新当前(s,a)的奖励值
- Sarsa(λ)会不断记录整条链路上的所有(s,a),在当进行奖励梯度传递的时候,会对整个成功路径上的所有(s,a)都进行Q-table的奖励更新
- 引入了历史路径(s,a)奖励衰减机制。本质上是消除算法早期随机尝试产生的错误方向,在算法中后期提高算法的整体收敛速度
- 离最终任务完成奖励越远的(s,a),其奖励更新权重就越低,因为早期的尝试中随机运动的比例比较高
- 离最终任务完成奖励越近的(s,a),其奖励更新权重就越高,因为理论上这些(s,a)对最终成功的帮助是更大的
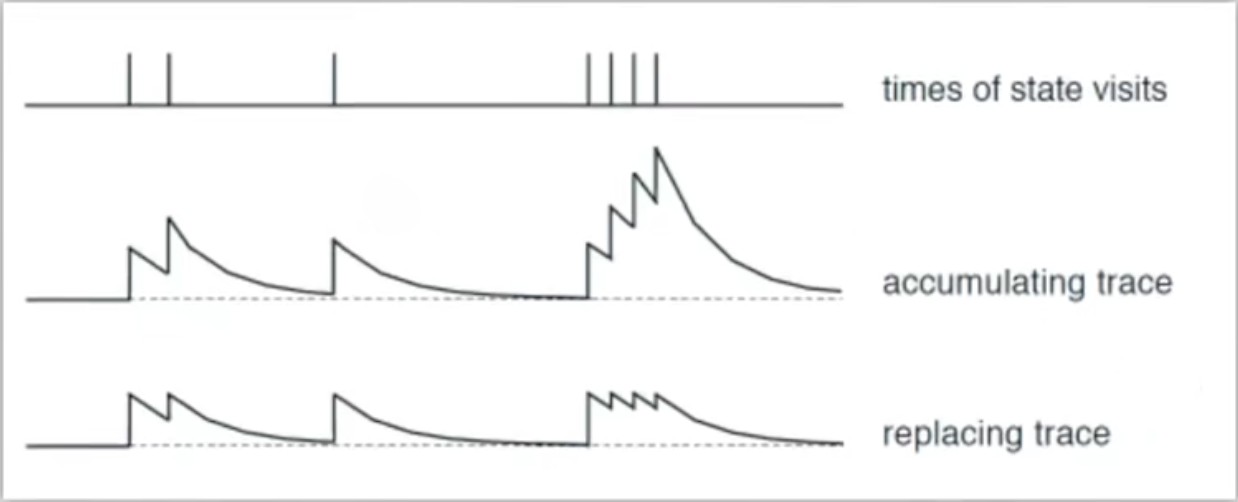
对于奖励更新机制来说,历史轨迹的奖励累计有两种方法,本质上是是否要对历史轨迹的奖励积累进行归一化:
- accumulating trace:对历史State选中的(s,a)每次都增加一个固定的价值奖励
- replacing trace:对历史State选中的(s,a)设定一个最大的奖励上限,防止历史路径中的某些对历史State选中的(s,a)奖励占比过大,导致整体算法过拟合
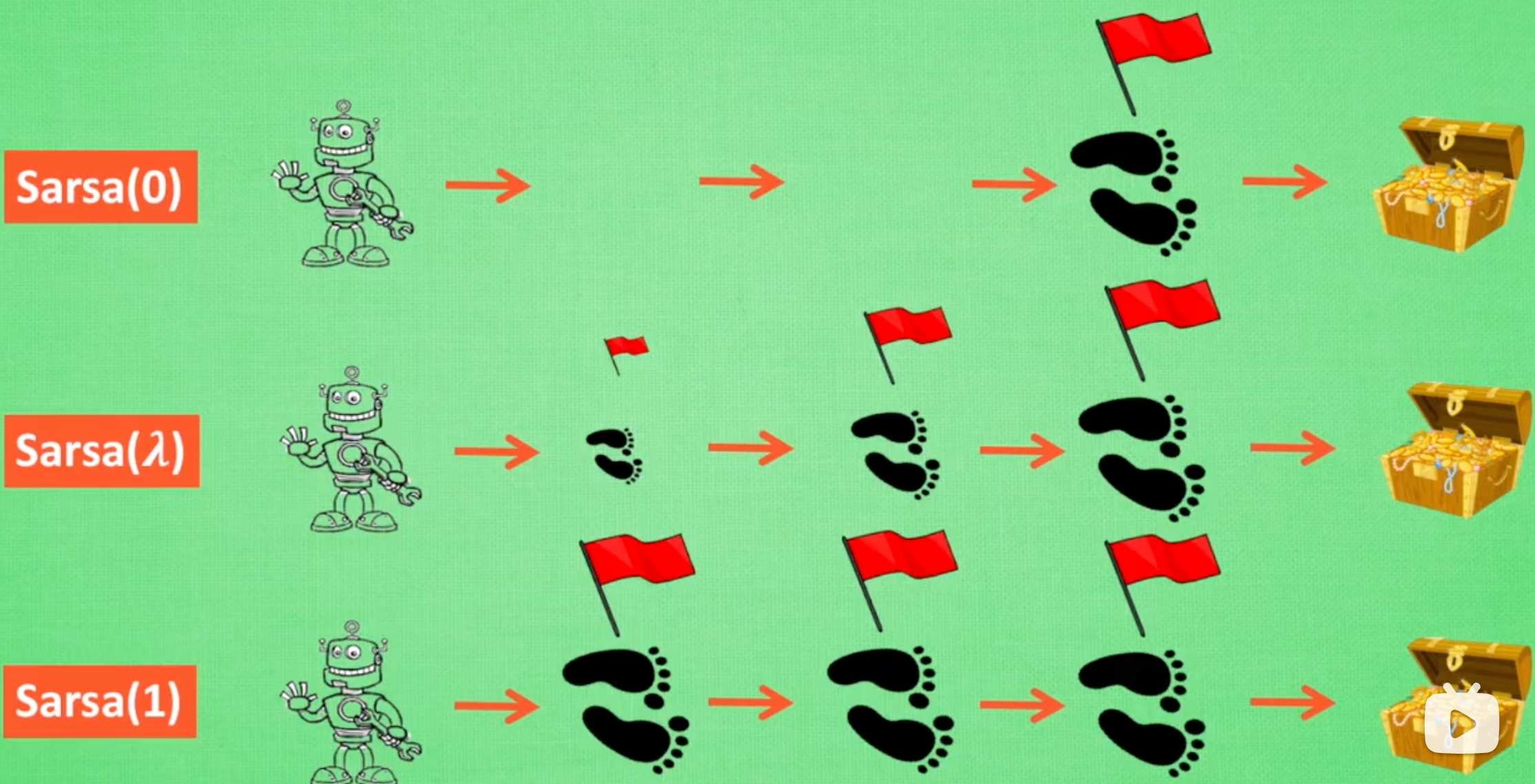
对于历史路径(s,a)奖励衰减机制来说,λ的不同取值,会带来不同的State权重衰减效果,本质是影响算法收敛速度。
- λ = 0 = 单步更新
- λ 属于 [0,1]:回合更新,离任务完成的终点越远,(s,a)更新权重越低;离任务完成的终点越近,(s,a)更新权重越高
- λ = 1:回合批量更新,每一(s,a)的更新权重相等
但Sarsa(λ)也存在一些问题:
- 当待探索的状态空间比较大的时候,Sarsa(λ)比较容易选择历史路径依赖,以为过早地给历史经验赋予了太高的奖励权重。最终陷入一个局部最优,甚至永远无法到达全局嘴有点
0x4:DQN案例
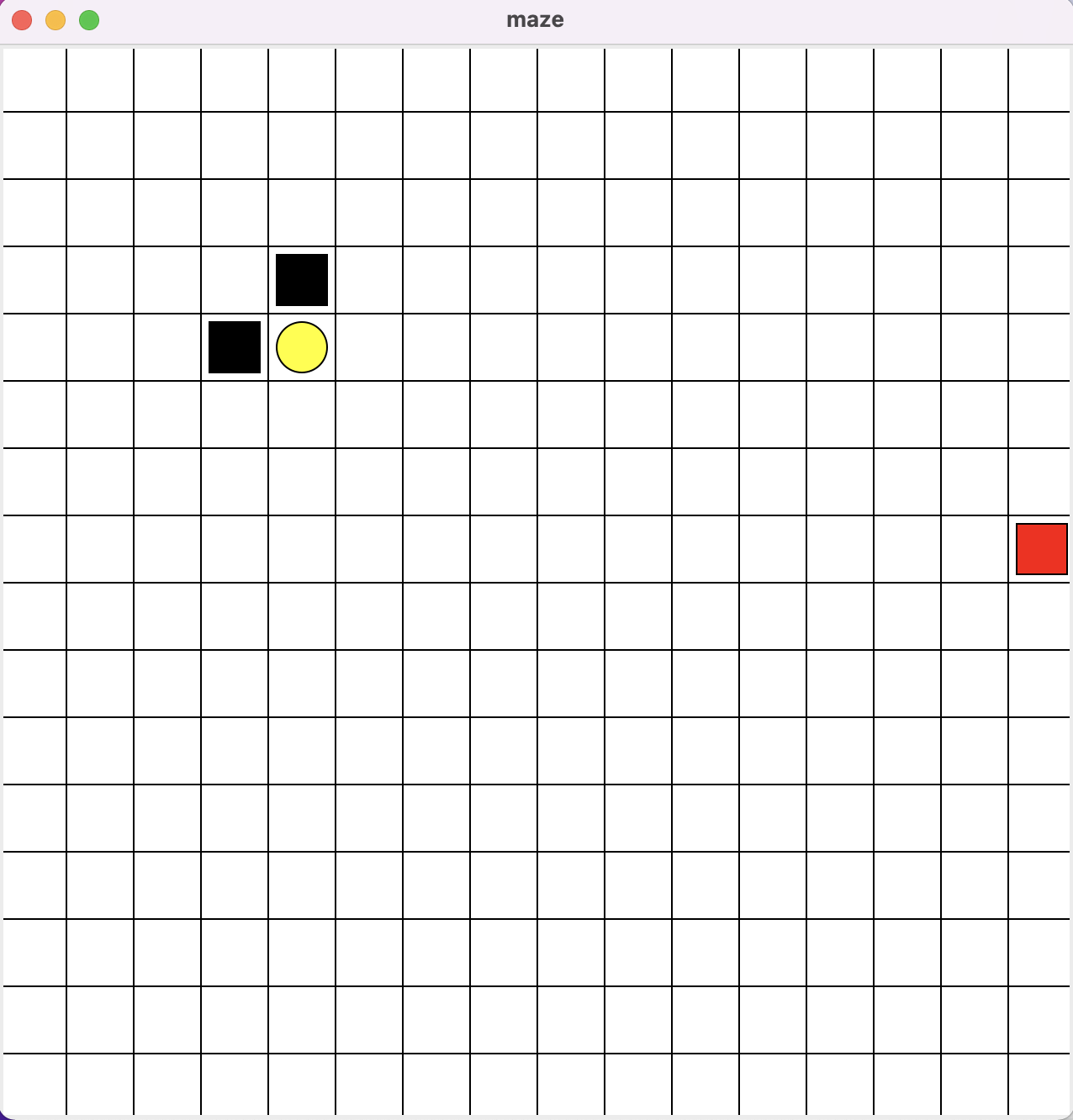
1、maze -- 用DQN训练一个跳方格游戏机器人
参考链接:
https://github.com/MorvanZhou/Reinforcement-learning-with-tensorflow/tree/master https://gymnasium.farama.org/ https://easyai.tech/blog/reinforcement-learning-with-python/ http://karpathy.github.io/2016/05/31/rl/ https://github.com/numpy/numpy-tutorials/blob/main/content/tutorial-deep-reinforcement-learning-with-pong-from-pixels.md https://github.com/tsmatz/reinforcement-learning-tutorials/blob/master/04-ppo.ipynb
如有侵权请联系:admin#unsafe.sh











