侧信道分析是一种十分强大的密码攻击手段,这种攻击手段可以追溯到第二次世界大战时期。它利用机器运算时内部产生的功率、辐射、热量等物理信号得到机器当前的内部状态,配合一系列算法可以获知受到保护的敏感信息。侧信道攻击可以用来入侵现实世界中的许多系统,缓存侧信道攻击则是一类和个人计算机、服务器关联度较大的攻击手段。现实中实施缓存侧信道攻击有着较强的条件限制,它要求攻击者与受害者十分接近,因此在这里我设置一个约束条件更少、更可行的攻击模型。
假设某国安全部门在追踪犯罪分子Bob的踪迹,他们通过鱼叉式钓鱼攻击将APT软件transmitter安装到Bob的个人计算机,企图通过transmitter搜集Bob电脑中的文件并传回到安全部门的秘密服务器。Bob是一个极具反侦查能力的人,他使用的操作系统具有信息流追踪的功能,这可以阻止transmitter回传文件。这种情况下Bob被诱导访问安全部门专门设置的一个网站,transmitter可以利用与该网站建立的CPU缓存侧信道进行通信,将比特流转换为网站JS代码访问内存的延迟,从而绕过操作系统的拦截。
1、缓存的层级结构
为了克服处理器运行速度和访存速度之间的不匹配,CPU中引入多级缓存的技术。现代Intel处理器通常分为3级缓存,即L1、L2、L3,缓存容量依次递增,访问延迟依次递增。Intel各层缓存的数据是嵌套的,L1是L2的子集,L2是L3的子集,AMD处理器的缓存架构是非嵌套的,不在本文的探讨范围内。根据Intel缓存嵌套结构我们可以得知,一旦某个数据被从L3中替换掉,那么它就会在各级缓存中消失,其作用相当于clflush指令。当处理器处理访存指令时,会首先访问L1,如果L1中找不到就会到L2中找,同理会到L3中寻找,如果L3中找不到则会到内存中找。每一次的cache miss消耗的时间为本级缓存的访问延迟+惩罚值,因此缓存的命中与否对于访存延迟有着极大的影响。


图1. Haswell缓存架构和Intel缓存嵌套结构
通过实验数据分析,缓存命中(L1命中)的访存延迟大约为40个时钟周期,而缓存未命中的访存延迟大约为275个时钟周期。L3缓存侧信道攻击就是利用这个明显的时间差异来判断当前L3 Cache的状态。

图2.两种情况下的访存延迟
2、L3 Cache结构
L3 Cache又被称为Last Level Cache(LLC),L1是通过虚拟地址来索引的,而L3是通过物理地址进行索引的,下面以典型的Intel core i7 4790处理器为例介绍L3的结构。i7 4790 L3 Cache由2048个cache set组成,每个缓存组又分为4个slice,每个slice由16个缓存行组成,因此缓存关联度为16,缓存总容量为:
64×16×4×2048=8MiB
图3.Intel core i7 4790的L3结构
从物理地址映射关系来看,L3的基本存储单元是64字节的缓存行,物理地址0~5表示缓存行内偏移,6~16位表示set index,一共有2048个set,6~31位经过一个未公开的哈希函数被映射为slice id,17~31位为tag位用来标记slice里面的缓存行。
图4.开启4KB分页下的L3地址映射
3、缓存替换算法
当L3 Cache发生cache miss时需要从内存中调取数据进入L3的某个slice,而此时如果slice已满则会导致某个缓存被写回(write back)内存,进而腾出空间给新进入的缓存行,这个替换策略就是缓存替换算法。Intel的第二代SandyBridge架构使用的是LRU替换策略,然而从第三代IvyBridge架构开始引入了自适应缓存替换策略(Adaptive Replacement Policies),该策略可以动态调整缓存替换算法使得L3的动态负载性能最优化。
由以上分析可知,地址address被映射到某个set的某个slice,如果能够找到其他16个映射到相同slice的物理地址,使用适当的遍历策略访问这16个地址就可以将address驱逐出整个缓存,这种方法可以达到与clflush指令的相同效果,我们将这16个地址组成的集合称为最小驱逐集(Eviction Set)。
Prime+Probe攻击的基本原理是,攻击者计算得到一个或者多个eviction set,通过测量遍历整个eviction set的时间得知是否有其他内存活动位于同一个缓存slice。基本步骤为:第一步计算得到eviction set,第二步为Prime阶段遍历eviction set填充整个缓存slice,第三步遍历整个eviction set得到总的访问延迟t1,第四步为Probe阶段,经过一段时间的等待后再次遍历eviction set得到总的访问延迟t2,如果这期间发生了缓存替换则t2 > t1,可知slice的状态发生了改变。以上原理很好理解,当第一步的eviction set被遍历后,里面所有的物理地址都被映射到特定的slice,缓存被设置为已知的状态,第二步中遍历eviction set得到的总时间t1也是所有地址都命中情况下的总体延迟,这个延迟值比较低,因为没有发生cache miss;当有其他访存活动需要用到这片slice时发生缓存替换,eviction set中某个地址上的数据被替换到内存,此时遍历eviction set就会发生cache miss,因此第三步中遍历eviction set得到的t2就是发生缓存失效时的总延迟,必然会t2 > t1。

图5.Prime+Probe的步骤
为了将Prime+Probe攻击应用到上述攻击模型,我写了分别写了两个程序receiver和transmitter。这两个程序通过L3 Cache建立侧信道,并且transmitter将需要发送的信息调制成一系列对特定内存的访问以改变L3 Cache的状态;receiver则计算出整个L3 Cache的所有eviction set,通过Prime+Probe监控整个L3 Cache的状态,拾取由transmitter造成的缓存状态改变并解调成比特位,最终通过拼接比特位还原出transmitter发送的信息。

图6.设计架构
receiver中第三步测量eviction set的遍历时间其实也还起到了填充slice的作用,因为遍历的过程本身就是eviction set的重新进入缓存slice的过程,每次的遍历不仅可以判断出transmitter是否发送比特位1,而且将缓存重置为已知的状态,为下一次的遍历做了准备。
1、Eviction Set的数据结构
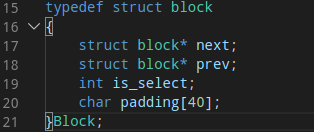
数据结构是算法的基础,在讨论计算Eviction Set之前先介绍他的数据结构。Eviction Set中的每一个元素是一个大小为64字节的双链表Block结构,大小正好可以用一个缓存行装下,表示一个缓存行,Block的首地址就是缓存行第一个字节的地址。前后指针用于链接其他元素形成一个双向链表,便于遍历和其他的链表操作;is_select字段为计算标位,这里不讨论;padding为40个字节的填充位。这里要注意的是,虽然每个字段加起来只有60字节(8+8+4+40),但是gcc编译器在编译时为了提高目标程序的访存效率会自动填充4个字节使之大小正好为一个缓存行。Eviction Set就是a个Block结构形成的双向链表(a是L3的关联度)。

图7.基本数据结构
2、计算Eviction Set
计算最小驱逐集是receiver的第一步,在Intel i7 4790处理器上,这个问题被转化为:计算出16个虚拟地址,使之映射到同一个slice。经过查阅国外实验室论文,目前最普遍的算法被称为Baseline Reduction。该算法的基本思想是:算法接收一个任意地址x和地址集合S作为参数输入,S可以将地址x从L3 Cache中驱逐但不是最小驱逐集。首先从S中取出任意地址c,测试地址集S-{c}是否仍能将x从缓存中刷新掉,如果S-{c}不能刷新x则表示地址c和x处于同一个slice,那么便将c记录到集合R中,如果S-{c}仍能刷新x则表示c是多余的,直接丢弃掉!需要注意的是测试地址集S-{c}是否仍能将x从缓存中刷新掉时(第4行)需要将集合R并入测试地址的集合,因为R中都是有效的地址。如此不断循环,直到R的元素个数等于L3 Cache的关联度a,表示此时从S中得到了最小驱逐集。

图8.Baseline Reduction的逻辑
这个算法的优点是容易理解而且使用C语言实现比较容易,但缺点也是显而易见,那就是时间复杂度为O(n2),随着S中元素数量的递增,总体耗时以平方级别递增,而S中元素的数量平均为3000,计算一个eviction set耗时约为15秒,用该算法计算整个L3 Cache在时间上的耗费显然是无法接受的。
算法改进:
这个问题可以利用抽屉原理来解决:问题转化为从集合S中选取特定的a个元素,假设给a+1个抽屉,将S中所有的元素任意分配到所有抽屉(每个抽屉必须有元素),那么至少有一个抽屉里不含特定的元素。通过逐个抽屉排除检查便可以逐步缩小搜索范围,集合S的大小按照 1 / |S| 的速率收敛,因此整个算法的时间复杂度为O(nlog(n)),当S中元素个数递增时,计算一个eviction set的耗费的时间大致线性递增,而且当|S| = 2048时,计算一个eviction set耗时控制在1秒以内,这相对于Baseline Reduction算法是一个极大地进步!

图9.抽屉原理
以下是抽屉递减算法的实现流程图,因为网络安全法的原因,在此我仅将流程图贴出,不讨论具体算法的实现!

图10.抽屉递减算法流程图
图10为在抽屉递减算法的作用下,初始驱逐集S的收敛情况,可以看出刚开始递减速度较快,越往后递减速度越慢。原因是S平均分发给每一个抽屉,每次排除掉的元素个数为 |S| / (a+1),越往后|S|越小,递减速率越慢。

图11.集合S的收敛情况
图11为使用抽屉递减算法计算64个eviction set耗费的时间为36秒,平均计算每个eviction set控制在了1秒以内!

图12.抽屉递减算法运行情况
3、Eviction Set的遍历策略
根据前面介绍,遍历eviction set有两个目的:第一,用eviction set的所有元素将slice填充满,将slice置为已知状态;第二,测量遍历时间,判断slice的状态。在SandyBridge架构的CPU中,由于缓存替换策略用的是LRU算法,该算法可以近似认为是线性的,换句话说我们可以准确控制将哪些缓存行替换出去(每次被替换掉的都是最近最久未使用的缓存行),因此只要沿着eviction set链表遍历一遍就可以确保slice里面之前的数据全部被替换为eviction set的元素。然而用了自适应替换算法的处理器,由于其替换算法是动态的,无法人为控制缓存行的替换过程,因此我设计了正向反向遍历的算法,利用多次正反向遍历,反复“刷洗”slice以达到大概率的填充slice目的!

图13.正反向遍历示意图
为了减少编译过程中的不确定性,我以内联汇编的形式设计了遍历算法。traverse函数接收Eviction Set的头指针作为参数,正反向遍历Eviction Set四次。其中第102行、110行既是发出访存信号将缓存行装入L3 Cache,又完成了指针的迭代,使遍历能够继续下去。第119行控制遍历的次数,正反算是一次遍历,这里一共是正反遍历4次。第105行、107行、113行、115行的lfence指令为内存屏障指令,目的是保护确保第102行、第110行访存指令完成后才执行后续指令,防止CPU的乱序执行造成影响。

图14.正反向遍历算法
4、数据的发送、拾取与处理
transmitter以比特位为单位向receiver “发送” 数据。如果当前发送比特位为1,则在时间TIME_INTERVAL内连续访问地址ones,此时receiver监控的相应slice就会产生较高的遍历延迟(Cache miss),相当于发送了一个高电平;如果当前发送比特位为0,则在TIME_INTERVAL时间内什么也不做,此时receiver监控的相应slice得到的遍历延迟处于正常水平(Cache hit),相当于发送了一个低电平。图15显示的是receiver监测到的L3 Cache的活动,图像底部高亮部分表示延迟值较高,蓝色部分为正常的延迟,此时的transmitter正在将字符 ‘q’ (二进制0111 0001)通过L3 Cache调制发送。

图15.receiver监测到的L3 Cache活动
实际transmitter在发送一个字节之前他会首先发送8个高电平(30行)它起到同步的作用,告诉receiver,8个高电平之后就是有意义的数据了可以准备好开始提取了。发送完一个字节之后transmitter空转8个TIME_INTERVAL,相当于发送8个低电平告诉receiver,字节已经发送结束。

图16.数据发送
根据transmitter的发送流程设计出receiver的数据提取算法,如果检测到的高电平持续时间超过7.5个TIME_INTERVAL则代表接收到的是transmitter发送的8个同步字节,这里为是么是7.5而不是8,是因为receiver进程可能滞后于transmitter进程,因此需要稍作微调。接下来用同样的方法根据检测到的电平持续的时间(TIME_INTERVAL)的倍数来检测出比特位1和比特位0。
注意,这里提到的 “电平” 并不是物理意义上的电压值,而是transmitter检测到的eviction set的遍历总延迟,高延迟用 “高电平”表示,意味着当前的slice的状态因为transmitter发送比特位 “1” 产生的内存访问导致了缓存替换,遍历eviction set的过程中发生了Cache miss;普通延迟用 “低电平” 表示,意味着当前slice的状态没有改变,遍历eviction set的过程中没有发生Cache miss,transmitter发送的是比特位“0”。
当前主要完成了计算Eviction Set的算法改进(我称这个叫“抽屉递减算法”, 听起来比较土),获得了计算效率的提升。
同时以 “抽屉递减算法” 为核心又写出了在可接受的时间范围内进行L3 Cache分析的 “缓存分析算法” ,并利用该算法得到的结果进行L3 Cache活动的监控,图15就是其中的一张效果图。
这个研究的核心就是 “缓存分析算法”,今后可以使用该算法获知某款Intel处理器的L3 Cache结构(可能6代及以后的CPU不行,具体没研究过因为没钱),进而利用侧信道分析实现一些特定的功能。
由于网络安全法的原因,这里仅仅分享和讨论我的技术研究成果而不公开项目的源代码!
[1] Theory and Practice of Finding Eviction Sets
[2] The Spy in the Sandbox: Practical Cache Attacks in JavaScript and their Implications
[3] Last-Level Cache Side-Channel Attacks are Practical
如有侵权请联系:admin#unsafe.sh