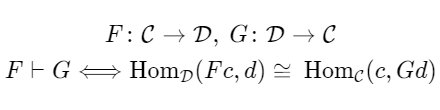
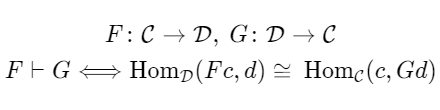
关于数学的诗般的文章。这不是特别技术性的。范畴论的知识很有帮助，但对于阅读来说并不是必需的。

我不会详细介绍这个定义，而且它在数学上并不严格，但我不会写出明显错误的东西，所以如果有明显错误的地方，如果你能指出来，那将会很有帮助。

后记：我对极限的左右方向搞错了，所以修正了

伴随的，反之亦然

在做数学的时候，人们会遇到伴随的概念。伴随是一个松散的逆概念。

反函数

我将以反函数为例解释反函数的概念和性质。如果你知道的话，你可以跳过它。

即使您没有遇到过伴随的概念，我想你们很多人都遇到过相反的概念。例如，函数的反函数。函数是接收实数的数据（如果您不知道实数是什么，只需将其视为包含小数的“数字”）并返回与接收到的值对应的实数。反函数是完全抵消 的影响的函数。这意味着如果再次传递一个值，它将始终等于原始值。

然而VS存在的条件却相当严格。因为即使丢失一点点信息，也无法消除效果。例如，“我把某个东西乘以0，结果是0，原来的数字是多少？”这个问题是无法回答的，因为乘以0的行为就相当于破坏信息的行为。逆数（即除以 0）不存在

现在假设函数的反函数是一个函数。也就是说，被完全取消，反之亦然。此时，和处于“完全平等的关系”。两者都可以将对方称为“自身的反面”。没有位置差别。

伴随函子对

在上面， 和被视为函数，但从现在开始我们将用函子代替它们。如果你写一个函子的解释，那就太长了，所以如果你不知道，请把它想象成一个函数之类的东西。ffggFFGG

与上一节一样，可以逆向思考函子，但是通过将其设为函子，就可以思考伴随的关系。当和处于伴随关系时，它们之间的左右位置存在差异。即使对于本质上不互逆的函子对，伴随也允许我们形成对。作为交换，它要求左右的立场不同，而不是完全平等的关系。我们表示是的左伴随（即，是的右伴随）。这次称为伴随函子对。

通过这种方式放松约束，在左右立场之间产生差异的同时，伴随的概念可以应用于比以往更多的对象。

事实上，任何概念都可以关联

伴随函子对的性质

假设函子和是伴随 ( )。此时，彼此之间可以说是建立了“镜像关系”。乍一看，两个行为完全不同的函子通过伴随的“镜子”以惊人的美丽对称性连接起来。

此外，函子的左（或右）伴随物如果存在则被证明是唯一的。由此可见，伴随关系并不是定义函子的部分属性，而是完整地描述了两个函子之间具有很强约束的关系。

如果和是伴随函子对，即使一个函子的信息被删除，它也可以从另一个函子中完整且唯一地恢复.并拥有必要且足够的信息来识别彼此。

换句话说，我们可以说 和 的复杂度本质上是相同的。

题外话：极限与伴随的关系

这是给那些了解范畴论但忘记了极限和伴随物之间关系的人（例如我自己）的注释。如果没有，请跳过。

• 模式是从下标类别到类别的函子（即函子类别的对象） 。
• 对角函子是将对象拟合到常数函子的函子。
• 图的极限是从到 的全态射T
• 图的余极限是通用态射T
• 如果任何类型的图都存在极限 (colimit)，则存在将图映射到极限 (colimit) 的极限 (colimit) 函子 ( )，并且它是对角线函子的右（左）伴随物。
• 即limit/colimit函子与对角函子之间存在如下关系：
• 有时也写成，但箭头方向与伴随词左右相反

概念左和右

现在开始追逐。正如我所写的，任何概念都是伴随的，我们可以在数学中的每个概念背后找到一对伴随函子。由于伴随有左和右的概念，因此每个概念都遵循左和右的概念。

然而，左和右仅与一对伴随函子相关，因此一个函子有可能既是“左”又是“右”（如）。另一方面，这样的例子并不多，所以确实有很多概念可以左右应用。

下面是左、右概念的例子，从简单到有些困难，大家都知道。对要么直接伴随，要么通过伴随函子序列连接（即它们具有相同的信息量）。

0 和 1

我们都知道，但仅仅因为我们都知道并不意味着这个概念很简单。事实上它们是非常有趣的数学对象。虽然0和1有多种类型，但这里我们将0和1视为自然数（即事物的数量）。在这种情况下，0 是左侧概念，1 是右侧概念。具体来说，中空图的余界和极限分别为 0 和 1（初始对象和终结对象、空集和单元素集）。

笛卡尔和与积（集合）

这个名字很令人困惑，但这个概念每个人都很熟悉。想象一下这样的情况：你有两个装满东西的袋子。此时，“将内容物收集到一个袋子中，然后取出一个”对应于Naokazu，而“将双手同时放入两个袋子中，然后将它们一一取出”对应于直接求和。直和是左边的概念，直积是右边的概念。具体来说，离散两点范畴下标的图的余极限和极限是直和和直积。对于集合，有时称为不相交和而不是直接和。

自由创作和遗忘

遗忘的意思是“忘记一些额外的数学结构”。例如，苹果是食物，但是如果忘记了食物的属性，就可能将其仅仅视为一种“材料” 。遗忘是丢失信息的行为。因此，相反的情况一般不可能存在。然而，以放松逆向的伴随词的形式，我们可以在遗忘的意义上想到“逆向” 。那是免费配置。遗忘是右边的概念，自由构图是左边的概念。

遗忘逆过程之所以不可能，是因为候选者不是唯一确定的。因为你无法确定你最初记住了哪些信息，所以你无法决定要回忆哪些信息。相反，如果我们能够正确地决定要回忆哪些信息，我们就可以定义遗忘的“逆向”。

自由配置提供了一种策略，可以在每种情况下从无数可能的弹性可能性中选择最合适的一种。通过选择可能的可能性中最“自由”的，我们从信息丢失的状态中独特地构造附加信息（因为丢失的信息当然无法恢复），即使你在忘记后进行了自由配置，一般情况下也会不能恢复）。

商和部分

“提取某物的部分”对应于“通过等价关系求商”。例如，让我们考虑“从所有整数中提取12 的倍数的行为”。这就是部分。结果是12 的倍数。与此相对应的行为是“将整个整数中的所有12的倍数相等的行为”。等同的意思是等同对待。结果是除以 12 后的余数。想象一下一个时钟。12 点 = 0 点。这就是商业。商对应于左边，部分对应于右边。

核和核

当存在扮演特殊角色（称为空对象）的实体时，就定义了内核和辅助内核的概念。地图的核心是“被碾压为0的部分”。另一方面，核是“图像的商（=整体复制时获得的部分） ”。很难理解，所以换句话来说，它的意思是“当整个图像被压缩到恰好为0时所剩余的空间” 。此时，核核对应于左侧，细胞核对应于右侧。A→BffAAffAAffBBBBffBB

笛卡尔积和幂

它与函数柯里化有很大关系。接受笛卡尔积并返回的函数可以等同于接受 a 并返回接受 a并返回 a 的函数。您可以将“接受并返回的函数”视为幂。左侧对应于给出笛卡尔积的行为，右侧对应于乘法的行为。

张量积和 Hom 函子

张量积对应于左侧，Hom 函子对应于右侧。

左右的概念及难点

到目前为止，我们已经看到了一些概念对及其左侧和右侧。这里有一个有趣的发现。而是“出现在左侧的概念对于人类来说往往比出现在右侧的概念‘困难’ ”。

0 和 1

对于人类来说，0 的概念比 1 的概念要困难得多。人类不是认识到某物存在，而是成功地认识到那里什么都没有，即虚无，并将其与存在（即大于或等于1的数字）放在同一水平上。处理数字的概念，很久之后。

直和与积

不仅在集合论中，在代数、几何等各个领域，直积都可以直观地解释为“取对运算”和“造对运算”。另一方面，直和（=共直积）是与直积左侧对应的概念，它的外观根据阶段而变化，有时表现得像直积，有时甚至需要复杂的构造其定义。

特别是在群论中，一般所说的“直和”与“直积对偶意义上的直和（=共直积）”是不同的。直和的行为很像群论中的笛卡尔积，但共直积对应于一个完全不同的概念，称为“自由积”。

题外话：尚和改变外貌的原因

事实上，直和没有一致的外观，而直积无论在哪个阶段都是一致的“配对运算”，这是有明确解释的。去除附加结构的遗忘函子是自由函子的右伴随函子，并且右伴随函子具有保留极限的性质。由于笛卡尔积是有极限的，所以取笛卡尔积的运算和忘记结构的运算是可交换的。因此，无论给集合添加什么样的数学结构，取笛卡尔积的运算都保证是“当看成集合时取一对的运算”。

另一方面，遗忘函子的右边很少有伴随函子（拓扑空间的范畴是个例外），所以一般来说，遗忘函子保留余极限，尤其是直和。我不这样做。因此，并不能保证“一套看时操作是一样的”，如果舞台改变，外观也会改变也就不足为奇了。

自由创作和遗忘

抛弃结构很容易。然而，从可能已经存在的结构中寻找并重建适当的结构的任务往往不是那么容易，而且从概念上讲，自由组合比遗忘更困难（这里不可能简单地解释到可能的程度）是困难的。自由构造函子，自由函子，被定义为遗忘函子的左伴随。

商和部分

当比较“商”的概念和“部分”的概念时，大多数人会发现“商”的概念更难以掌握。事实上，我怀疑很少有人会不同意“商集”的概念比“子集”的概念更困难。

普通理科生几乎没有不知道“向量空间的子空间”这个概念的，但了解“向量空间的商空间”的人却不多。我怀疑许多大学（除非他们在数学系）甚至没有在线性代数课程中包含商空间。同样，在拓扑空间理论中，部分拓扑是教科书中一定会出现的概念，而商拓扑则不一定会出现在教科书中。

然而，正如伴随函数一章中所解释的，这些概念通过伴随函子连接起来，即它们本质上具有完全相同的数学复杂性。尽管如此，商和部分这两个方面给人类带来的复杂性印象却是截然不同的。

核和核

这也是一样的。核（kernel），也称为核（kernel），是线性代数中常用的概念，就像肢体一样，但核（cokernel），即核的对偶，却很少受到关注。

Cokernel 在模和同调代数等领域也很活跃，但除非您是数学学生，否则通常不会深入接触这些领域。

张量积和 Hom 函子

这通常也被认为是比张量积更难的概念。Hom 函子的名字可能并不广为人知，但基本上它只是说“取连接两个对象的所有态射

微妙的例子

到目前为止，我见过一些看起来“左侧更难”的例子，但并非所有情况都是如此，而且有一些情况是微妙的，甚至看起来是相反的。

遗忘函子的右伴随

通常，遗忘函子的左伴随是自由函子，但在拓扑空间范畴中存在遗忘函子的右伴随。这也是一种自由组合，在 的情况下，相当于在集合中放入了一个相干拓扑。如果出现这种情况，那么遗忘和自由作文在难度上似乎就没有什么区别了。

此外，当存在全称量词和存在量词、完全图和无边图等极端琐碎结构时，似乎常常存在遗忘函子的左右伴随。确实，如果要介绍的结构是不言自明的，我觉得和忘记结构在难度上没有太大区别。

笛卡尔积和幂

给出直积的函子和将其向左和向右提升的函子是伴随的。就我个人而言，我认为在概念上创建对比考虑指数更容易，但笛卡尔积位于左侧。

差异原因

为什么左、右概念理论上复杂度完全相同，但理解难度却存在差异？

这个问题我还没有得到明确的答案，但我认为“数学本身”或者“人类的思维方式”是有一个本来的方向的，违背它的概念是人类所理解的。我已经平静了直到理解这一定是痛苦的。

从数学上来说，我们知道它们具有相同的复杂性，因此我们只能在数学“之外”寻找答案。或者，也可以制定人类思维和数学的方向，然后在此基础上制定关于数学难度的理论。

我认为人类是一种神秘的生物。