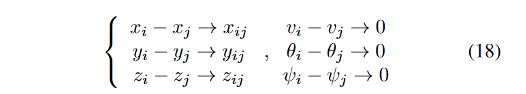
团队科研成果分享

2023.11.27-2023.12.03

01

研究背景

近年来，自主式水下航行器(AUV)集传感器探测、信息融合和航行器控制等技术于一体，已成为复杂水下环境中执行作业任务的必备工具，如资源勘探、环境监测，数据收集，和水下战争等。然而，越来越复杂和大规模的水下作业需要多个AUV的合作，这带来了许多科学挑战。本文针对AUV编队协同路径规划问题展开研究，旨在规划安全、节能的AUV路径以支持AUV编队在复杂三维水下空间中的运动，并驱动AUV在路径上运动的同时保持预定义的队形结构。

麻雀搜索算法（SSA）采用了警告机制来防止搜索过程陷入局部最优，这是大多数群智能算法的共同问题。SSA模拟了麻雀群体在寻找食物时的行为，尽管在探索能力和收敛速度方面优于传统的群智能算法，但在提高搜索精度和三维空间应用的精确程序方面仍有进步的空间，特别是在解决协同编队运动的路径规划问题时。采用现代算法对多无人车协同运动的各种路径进行优化的方案相对有限，因为传统的队形运动方法往往迫使队形成员在协同运动中遵循特定的曲线。然而，在AUV编队协同运动的路径规划问题中，由于AUV运动的非线性和不确定性以及三维水下地形的复杂性，精确地保持预定的编队构形存在许多挑战。为了使AUV形成编队，需要规划引导AUV到达特定位置形成编队的三维路径，同时还要选择合适的策略保证AUV的位姿一致性，并在AUV编队运动过程中保持运动状态的一致性，从而实现编队避障。

02

关键技术

本文提出了一种面向协同AUV系统编队运动的路径规划方法，即基于一致性SSA的编队路径规划( CSFPP )。CSFPP采用改进的SSA规划AUV编队的全局路径，然后将输出路径融入到引入APF的共识算法中，以实现编队成员的协同运动。简而言之，它的工作如下。

在全局路径规划步骤中，CSFPP继承了一种改进的SSA，在初始化麻雀种群时采用佳点集，并在每次算法迭代中采用黄金搜索优化(GSO)来更新探索器的位置。然后，根据算法在一次迭代过程中发现的最优解，为每次迭代过程分配自适应搜索策略，以平衡局部开发和全局探索，防止局部最优现象。在编队运动阶段，采用共识算法实现AUV之间的协调与协作，保证编队成员的一致性，并利用各AUV与障碍物之间的APF机制，引导成员跟随全局路径，避开障碍物，恢复队形。

本文的主要贡献如下：

1 )本文提出了一种编队路径规划与协同运动方法CSFPP，旨在引导AUV编队穿越地形复杂的水下环境。CSFPP由用于AUV编队整体路径规划的改进SSA和用于在运动过程中稳定编队的带有APF机制的共识算法组成。

2 )针对AUV编队全局航路规划问题，提出了一种基于GSO的自适应SSA (GASSA)，利用GSO平衡局部开发和全局探索能力，并采用自适应搜索策略防止算法迭代过程中出现局部最优现象。

3 )研究的目标是引导AUV在具有挑战性的环境中保持稳定的队形和跟踪预定的轨迹。为此，CSFPP引入了一种基于共识算法的编队控制方法。为了保持形体在运动过程中的稳定性并实现自主避障，所提出的方法包括APF机制和自主避障机制。

03

算法介绍

一、系统模型

图1 编队运动的实例场景

A. 优化目标

在确定基于群体智能的水下路径规划的目标函数时，必须考虑海洋地理和运动学约束的综合影响。本研究将水下地形、避障、路径长度和转弯角度等约束条件考虑到目标函数中，用移动成本( f1 )、安全成本( f2 )和转弯成本( f3 )表示如下。图2给出了一个AUV轨迹的例子，表示为D个航路点的列表。三维环境中第i条路径上第j个航路点的位置用P_{ij}=(x_{ij},y_{ij},z_{ij})表示。相应地，移动成本f1由式(1)表示。

图2 AUV运动轨迹示例

安全成本f2与水下障碍物和海底地形有关，水下障碍物用球形区域来衡量，海底地形用水下山脉的范围来衡量。

式中：k为路径中障碍物的个数；dk是AUV与障碍物之间的距离；和Rk为表示障碍物的球形区域半径，如图3所示，dsf为AUV与障碍物之间的安全距离，保证AUV与障碍物之间不会发生碰撞，当AUV与障碍物之间的距离小于dsf时，安全成本呈指数增长。zi和z(xi, yi)分别是AUV的z坐标和沿轨迹地形最高的航点。

图3 安全成本的距离变量

如下图4和式(5)。(5)表示转弯代价f3，它由AUV在水平和垂直转弯行为中产生的能量代价组成，与艏摇角(ψ)和俯仰角(θ)有关：

图4 转弯成本角度变量

其中α是衡量水平转向行为和垂直转向行为之间能量代价的因素。最后，描述了评价最优路径的优化函数F：

式中：N为可用路径数；W1、W2、W3为目标函数中各成本的权重，根据应用需求进行调整，总和为1；C1，C2和C3是用于归一化目标函数中的成本值的常数。

B. 编队运动模型

  该部分介绍了AUV运动模型，图5所示为AUV运动控制所采用的坐标系，包括惯性坐标系 -ξηζ和固定坐标系O-xyz。

图5 坐标系示意图

二、共识-麻雀搜索算法 

本节将介绍所提出的CSFPP，它结合了一种改进的路径规划SSA和一种基于共识算法的编队控制技术。

A. 基于黄金搜索优化的自适应麻雀搜索算法

SSA随机初始化种群可能导致有限的种群多样性，从而减慢收敛能力，并在高维解空间中触发局部最优。因此，GASSA采用佳点集进行初始化，以保证种群多样性。然后在后续更新探索者位置的阶段，使用GSO来利用多样化的种群来平衡局部开发和全局探索能力；并采用自适应搜索策略更新侦察机的位置，动态控制侦察机的步长，防止陷入局部最优。具体内容如下所述。

1 )基于佳点集初始化种群：佳点集与空间维度无关，非常适合于保证高维空间中均匀稳定的点选择。在GASSA中，解空间的维数与组成AUV路径的航路点数相关。通过用佳点集初始化种群，可以提高对高维问题的求解能力，以发挥AUV在大规模水下环境中路径规划的优势。

2 )基于黄金搜索优化的发现者位置更新：根据公式发现者原始位置更新公式，当R2 < ST时，探险者周围没有捕食者，允许进行广泛的探索。然而，它在迭代后期容易导致种群的聚集，从而降低了种群的多样性和探索能力，同时也降低了全局搜索和局部搜索之间的平衡。为了解决这些问题，在迭代阶段使用GSO来更新探索者的位置。

GASSA将GSO应用于使用步长因子来分配探索者，步长因子用下式表示。

其中c1和c2是服从均值为0，方差为1的正态分布的随机数；r1和r2是0到1的随机数；X_{best}^{t_i}为当前迭代的全局最优位置；X_{best}^{t_i}是到当前迭代为止的全局最优位置；是步长因子，它控制着侦察机的移动距离；和T是一个转移算子，由下式给出。

w是一个常数。在算法迭代初期，麻雀主要进行广泛的探索，较大的变换算子有利于全局搜索。在后期迭代中，当大部分麻雀移动( R2 < ST)不大时，利用高斯分布函数和正余弦函数的系数对麻雀种群进行扰动，防止种群聚集。转换算子T将搜索从探索转换为利用，以控制迭代前期的全局探索和迭代后期的局部开发之间的平衡。

3 )通过自适应搜索策略更新侦察者的位置：变量K以方程中的最佳适应度值控制侦察者的步长，变量β控制了其他侦察者的步长。在这种情况下，较高的β值有利于全局搜索，而较小的β值有利于局部开发。然而，由于β的变化服从正态分布，如果经过多次迭代后适应度值fg变化不大，算法可能会陷入局部最优。因此，提出的 GASSA 对流程进行了如下修改。

其中a是随机赋值为1或- 1；F是估计潜在局部最优的一个阈值；E是一个控制收敛速度的因子，在我们的情况下取为1/2；而fdiff是给定迭代次数的适应度值之差的均值，表示为：

式中ts为监测适应度值变化的次数。通过自适应地分配步长因子，使位于种群中心的麻雀在算法搜索停滞时设置更大的步长，从而探索更大的搜索空间，跳出局部最优。其他时间利用余弦函数和随机值引入小扰动，从而提高局部开发的精度。

B. 基于共识算法的编队控制

一旦GASSA确定了路径，下一步就是控制AUV在路径上进行编队运动，目标是引导AUV编队在障碍物环境中保持指定队形的同时保持方向和速度一致。在本文中，我们以菱形结构编队(图6)为例描述了编队运动方法，其中一个领航AUV放置在编队的中心，每个角落放置四个成员AUV。本文使用菱形结构编队的目的是保证成员AUV之间直接的信息交换和更新，同时允许成员AUV立即访问领导者AUV的轨迹信息。然而，该算法也可以在不同的队形结构下发挥作用。

当AUV编队稳定时，需要满足以下条件。

其中i和j是相邻的 AUV；v为AUV在三维空间中的速度状态；θ为偏航角；ψ 为俯仰角；xij、yij、zij 分别为相邻 AUV 之间在 x、y、z 轴方向上的距离。

图6 菱形结构编队

该方程约束每个方向上AUV的相对位置应该收敛到根据期望队形设置的预定距离，并且每个AUV的速度和偏航角、俯仰角应该接近相同的值。然后，基于二阶积分器系统，AUV的运动状态可以用微分方程描述如下。

其中ni为运动状态，经过求导后输出AUV的速度vi；N为AUV成员个数；其中ui为控制输入，由AUV的速度决定，包括线速度和角速度。最后，根据AUV的运动学方程，给出了控制编队的算法：

其中aij(=0或1)是一个参数，表示AUV i和另一个成员j是否能够交换状态信息；b_i(= 0或1)表示第i个AUV能否从领航者那里获取所需参考轨迹的信息；a是调节其他成员控制速度的增益因子，通常设置为1；∆ij为AUV的期望状态∆^d是参考轨迹的信息。式( 20 )考虑了编队调整过程中出现的控制偏差，通过比较领航AUV的参考轨迹信息，使编队在跟随GASSA确定的轨迹的同时达到期望的结构。

在AUV编队中，领航AUV遵循无障碍轨迹，但成员AUV如果靠近领航者的轨迹，可能会遇到障碍物。因此，在编队导航过程中引入了APF机制。选取的人工势场模型如下：

其中Uij表示AUV之间的势场力函数，Uio表示斥力场力函数在AUV和障碍物之间，rij是两个AUV之间的距离；R是平衡APF的一个参考值，当rij等于r时，AUV之间的吸引力和排斥力达到平衡；Rio为AUVi与障碍物之间的距离，ro为障碍物斥力场的影响范围。

当AUV成员遇到障碍物( rio < ro)时，排斥力将AUV推离障碍物，AUV随后跟随AUV编队中APF的联合吸引力。这种方法可以引导AUV成员灵活地避开障碍物，但可能会混淆一致性算法，从而破坏编队控制。因此，本文提出了一种虚拟点的方案来避免这个问题，图7对此进行了说明。

图7 碰撞危险实例(a)和避障实例(b)。

图7显示了使用虚拟点方案的避障。当AUV1运动到其与障碍物的距离小于安全距离的位置时，排斥力将其推离障碍物，AUV编队将虚拟点放置到属于AUV1的位置。同时，虚拟点和其余AUV触发对AUV1的引力，从而产生联合引力，引导AUV1在其他AUV越过障碍物后重新加入编队；并且在AUV1返回之前，剩余的AUV将与虚拟点一起执行共识算法，使得AUV编队的运动始终保持稳定。

04

实验结果

本部分对CSFPP的性能进行了分析。首先，对GASSA的收敛性能进行了测试，并与经典算法和最近提出的算法进行了比较。接下来，在仿真环境中考察了基于编队运动方法的共识算法的性能。

1、GASSA的收敛性能

实验环境：使用CEC 2022中的5个基准测试函数对GASSA进行测试。通过鲸鱼优化算法( WOA- 2017 )、蛇优化算法( SO- 2022 )、SSA ( 2020 )、混沌策略自适应惯性权重策略SSA (CASSA- 2021 )、多策略改进SSA( MSSA- 2022 )及RL-PPO对GASSA的性能进行比较分析。

图8说明了GASSA在F1上达到了最快的收敛速度，在迭代初期达到了最优值。图9中，对于10维的基本函数F3和F5，GASSA、MSSA和CASSA的收敛性能相当。然而，值得注意的是，在20维的情况下，MSSA和CASSA的收敛速度比GASSA慢，这表明通过使用佳点集初始化种群和GSO分配种群，GASSA的高维搜索性能得到了改善。在图 10中，GASSA 最初对于混合函数 F7 表现出较慢的收敛速度，但在超过100次迭代后，其收敛性能超过MSSA和CASSA，表明所提出的自适应搜索策略在防止局部最优现象方面具有优势；而在图11中，GASSA在F11的10维和20维均表现出与SSA、MSSA和CASSA相近的性能，但在迭代后期具有更高的收敛精度。此外，还将六种不同算法得到的最优值与理论值进行了比较。图12 (a)和(b)分别给出了10维和20维情形下算法找到的最优值与理论最优值的比值(F′) .实验结果表明，在10维场景下，MSSA和CASSA具有与GASSA相近的近似性能。但在20维时，GASSA的性能优于MSSA和CASSA，达到了F5和F7，显示了其优越的寻优能力。

图8：单峰函数F1的收敛性能比较.

图9：多峰函数F3和F5的收敛性能比较。

图10：混合函数F7的收敛性能比较。

图11：合成函数F11的收敛性能比较.

图12：六种算法的最优值与理论最优值之比的直方图

2. CSFPP的仿真性能

为了验证CSFPP的有效性，本文进行了路径规划的对比仿真，并在本小节对基于强化学习的路径规划方法进行了额外的对比，以进一步分析路径规划的性能。仿真中的RL采用近端策略优化( PPO )框架，其中CSFPP的优化目标与PPO的奖励函数相关联，考虑了安全性和移动性性能。仿真环境为500m × 500m × 500m的水下空间，有水下山体和随机放置的球形障碍物。AUV的初始速度设定为4m / sec，并以± 2m / sec的速度变化以保持队形。

图13：3D环境下路径的比较

7种算法的3D路径在图13中进行了比较。从图中可以看出，WOA、SSA和SO在靠近障碍物的区域会产生突然转弯的轨迹，这是由于局部最优导致转弯成本增加。MSSA，CASSA和提出的GASSA产生了相对平滑的轨迹，GASSA输出了最低的移动成本，如表4所示。

表4比较了成本构成和7个算法的执行时间。结果表明，GASSA生成了一条安全平滑的路径，其长度与预期一致，并且执行时间最短，因为GSO应用于探索者分布平衡了局部开发和全局探索，加速了算法的收敛。RL-PPO得益于生成平滑路径的实时环境信息，在安全性和转弯代价方面表现出良好的性能，而基于采样的群智能方法在移动代价方面仍然表现得更好，而移动代价是由整体路径长度决定的。这是因为复杂的障碍物环境为RL-PPO提供了有限的行为空间。

然后，对基于共识算法的编队控制进行了仿真，如图14和15所示，其中四个AUV围绕领航AUV形成菱形编队，初始状态分别为η1 = [10, 10, 30, 3, 2]T, η2 = [30, 30, 10, 2, 2.5]T, η3 = [30, 80, 20, 4, 2]T 和 η4 = [50, 30, 10, 1, 2]T，并遵循分配给领航AUV的参考轨迹。

在图中，起点随机分布的跟随者跟踪参考轨迹，并在P1处通过共识算法形成编队。航行一定距离后，来自障碍物的APF推动AUV2和AUV3在P2处离开编队，但其余AUV仍以虚拟点方案保持编队队形。在P3时，虚拟点的APF将AUV2和AUV3拖回编队，然后AUV通过共识算法继续编队运动。

图14：菱形AUV编队的路径。

图15：菱形AUV编队的路径(反面)。

最后，图16和图17展示了AUVs在五个自由度上的位姿一致性误差，Y轴是AUVs的实际状态与它们在编队中应该处于的状态之间的偏差。从图中可以看出，在65秒左右误差收敛到0，这意味着四个AUV已经完成编队，然后AUV2和AUV3在遇到障碍物时误差在90秒左右发生变化，APF然后在140秒左右，他们恢复了误差再次收敛到0的形式。共识算法使得AUV在编队开始时误差变化平缓，但当AUV编队通过障碍物区域时，误差变化变得粗糙，这是由于基于APF的避障比基于共识算法的编队控制具有更高的优先级，迫使AUV立即离开障碍物。

图16：AUV的位置误差       

 图17：AUV的姿态误差

05

总结

本文提出了一种多AUV水下编队路径规划方法CSFPP。它包括两个阶段，基于群体智能的路径规划算法( GASSA )和基于共识算法和APF的编队控制方法。GASSA是对SSA的改进，通过减少局部最优现象和平衡局部开发和全局探索来提高优化，而编队控制方法则是将GASSA的输出作为参考路径，在保持队形和躲避障碍物的同时，引导AUV沿着路线前进。通过与CEC 2022中的部分函数进行收敛能力对比，验证了GASSA的改进性能；并通过水下仿真验证了CSFPP的整体性能，包括路径规划、编队控制和避障。

扫描二维码关注我们