By Joop van de Pol
Trusted execution environments (TEE) such as secure enclaves are becoming more popular to secure assets in the cloud. Their promise is enticing because when enclaves are properly used, even the operator of the enclave or the cloud service should not be able to access those assets. However, this leads to a strong attacker model, where the entity interacting with the enclave can be the attacker. In this blog post, we will examine one way that cryptography involving AES-GCM, ECDSA, and Shamir’s secret sharing algorithm can fail in this setting—specifically, by using the Forbidden attack on AES-GCM to flip bits on a private key shard, we can iteratively recover the private key.
Trusted Enclaves
TEEs come in all shapes and sizes. They can be realized using separate secure hardware, such as Hardware Security Modules (HSM), Trusted Platform Modules (TPM), or other dedicated security chips as part of a system on chip (SoC). It’s also possible to implement them in hardware that is shared with untrusted entities, using memory isolation techniques such as TrustZone or a hypervisor. Examples in this category are secure enclaves such as Intel SGX, Amazon Nitro, etc.
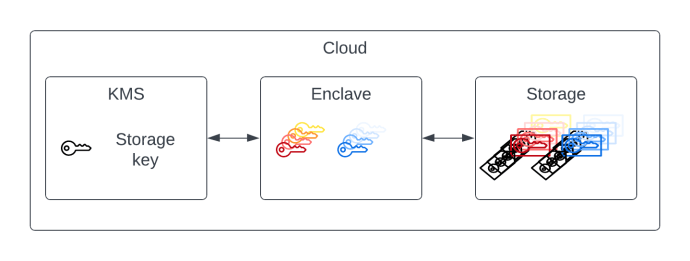
One challenge secure enclaves face is that they have little to no persistent memory, so large amounts of data that need to be available across power cycles must be stored outside the enclave. To keep this data secure, it must be encrypted using a storage key that is stored either inside the trusted environment or inside an external Key Management Service (KMS) that restricts access to the enclave (e.g., through some form of attestation).
Figure 1: Design of a typical secure enclave, where encrypted data is stored outside the enclave and the data encryption key is securely stored outside the enclave in a KMS
However, because the data is stored externally, the untrusted entity interacting with the enclave will see this data and can potentially modify it. Even when using strong cryptography such as authenticated encryption—typically Authenticated Encryption with Additional Data (AEAD)—it is very difficult for the enclave to protect itself against rollback attacks, where the untrusted entity replaces the external data with an earlier version of the same data since both of them will pass authentication. A tempting solution would be to version data stored externally to the enclave, but because the enclave is stateless and doesn’t know what the latest version should be, this quickly becomes a chicken-and-egg problem. Therefore, keeping track of version numbers or usage counters in this setting is difficult, if not impossible.
Signing in a trusted enclave
One interesting application for trusted enclaves is holding digital signature private keys (such as ECDSA keys) to perform signing. If set up correctly, no one can exfiltrate the signing keys from the enclave. However, because the signing keys must be available even after a power cycle of the enclave, they must typically be stored persistently in some external storage. To prevent anyone with access to this external storage from obtaining or modifying the signing key, it needs to be encrypted using an AEAD.
Figure 2: Design for signing with a trusted enclave, where the encrypted signing key is stored outside the enclave and encrypted with a key protected and managed by a KMS
Enter everyone’s favorite AEAD: AES-GCM! Due to its brittle design, the authentication guarantees are irrevocably broken as soon as the nonce is reused to encrypt two different signing keys. Because the AES block size is limited to 128 bits and because you need 32 bits for the counter, you have only 96 bits for your nonce. No worries, though; you just have to make sure you don’t invoke AES-GCM with the same secret key using random nonces more than 232 times! So the enclave just has to keep track of a usage counter. Alas, as previously stated, that’s basically impossible.1
Figure 3: Preventing AES-GCM misuse in an enclave requires maintaining state to monitor AES-GCM usage and must prevent rollback attacks where an attacker replays an old state, though this is difficult to achieve in practice.
So an attacker can have the enclave generate an arbitrary number of signing keys, all of which it must encrypt to store them externally. Eventually, the nonce will repeat, and the attacker can recover the AES-GCM hash key using the Forbidden attack. The details are not very important, but essentially, with the AES-GCM hash key, the attacker can take any existing AES-GCM ciphertext and tag, modify the ciphertext in some way, and use the hash key to update the tag. Specifically, they can flip bits in the ciphertext, which, when decrypted by the enclave, will result in the original plaintext except that the same bits will be flipped. This is not good. But how bad is it?
Attacking ECDSA signatures
The attack is not specific to ECDSA, so understanding all the specific mathematics behind ECDSA is not required. The only important background needed to understand the attack is an understanding of how ECDSA key pairs are constructed. The private key corresponds to a number (also called a scalar) d. To obtain the corresponding public key Q, the private key is multiplied by the base point G of the specific elliptic curve you want to use.
Q = d · G
By leveraging the broken AES-GCM authentication, the attacker can flip bits in the encrypted private key and have the enclave decrypt it and use it to sign a message. As the encryption part of AES-GCM is essentially counter mode, flipping bits in the encrypted private key will cause the same bit flips in the corresponding plaintext private key.
Figure 4: By modifying the ciphertext stored in external storage, an attack can cause the secure enclave to sign messages with a modified key without having to target the enclave itself.
What happens when we flip the least significant bit of the private key? A zero bit would become a one, which is equivalent to adding one to the private key. Conversely, a one bit would become a zero, which is equivalent to subtracting one from the private key. Essentially, the effect that the bit flip has on the private key depends on the unknown value of the private key bit.
That’s great, but how can we know which of these two options happened without knowing the private key? Well, if we generate a signature with the flipped private key, we can verify the signature using a modified public key by adding or subtracting the generator. If it verifies with the added generator, we know that the private key bit was zero, whereas if it verifies with the subtracted generator, we know that the private key bit was one.
(d + 1) · G = d · G + G = Q + G
(d – 1) · G = d · G – G = Q – G
We can now repeat the process to recover other bits of the private key. Instead of adding or subtracting one, we’ll be adding or subtracting a power of two from the private key. By adding or subtracting the corresponding multiples of the generator from the public key, we learn a new bit of the private key. It’s not strictly necessary to recover one bit at a time. You can flip multiple bits and try signature verification based on all the possible effects these flipped bits can have on the private key.
Splitting the bit
Interestingly, the attack still works when the private key is split into different shards using Shamir’s secret sharing algorithm before encryption. The enclave receives the different encrypted shards, decrypts them, recombines the shards into the private key, and then signs. As a result, we cannot directly flip individual bits in the private key.
But what happens when we flip a bit in one of the shards? In Shamir’s secret sharing (see also our excellent ZKDocs article on this topic), each shard consists of a pair of x and y values that are used to interpolate a polynomial using Lagrange interpolation. The secret value is given by the value of the interpolated polynomial when evaluated at x = 0.
Flipping bits in one of the y values changes the interpolated polynomial, which corresponds to a different secret—in our case, the private key. Basically, recombining the secret corresponds to a sum of weighted y values, where each weight is a Lagrange coefficient λj that can easily be computed from the x coordinates (which are typically chosen to be consecutive integers starting from one up to the number of shards).
Putting all this together, flipping bits in one of the shares adds to or subtracts from the share, depending on the value of the bit. This then results in adding or subtracting a multiple of the corresponding Lagrange coefficient λj from the private key. By generating signatures with this modified private key and validating them using modified public keys, we can recover the values of the secret shares bit by bit. After obtaining the shares, we can recombine them into the private key. All in all, this shows that the enclave operator could extract the private key from the enclave, despite all the cryptography and isolation involved.
Final bit
As this exploration of the Forbidden attack on AES-GCM in secure enclaves reveals, cryptographic primitives such as AES-GCM, ECDSA, and Shamir’s secret sharing, while generally robust, may still be vulnerable if deployed incorrectly. The complexity of TEEs and the evolving nature of adversarial methods make safeguarding sensitive data a difficult task. At Trail of Bits, we understand these challenges. Using our deep expertise in cryptography and application security, we provide comprehensive system audits, identifying potential vulnerabilities and offering effective mitigation strategies. By partnering with us, developers can better avoid potential cryptographic pitfalls and improve the overall security posture of their TEEs.
1 You could argue that, in this toy example, the KMS could keep track of the usage counter because it controls access to the storage key. However, in practice, the KMS is usually quite limited in the type of data it can encrypt and decrypt (typically only cryptographic keys). It is likely not possible to encrypt secret key shards, for example.