By Jim Miller

We’ve updated ZKDocs with four new sections and additions to existing content. ZKDocs provides explanations, guidance, and documentation for cryptographic protocols that are otherwise sparingly discussed but are used in practice. As such, we’ve added four new sections detailing common protocols that previously lacked implementation guidance:

We’ve also added a new subsection to our random sampling section that details an effective random sampling technique known as wide modular reduction. This technique is well known in certain cryptographic circles but to our knowledge has not been widely publicized.

This post summarizes each of these additions at a high level.

ICYMI: What is ZKDocs? Almost two years ago, we first released our website ZKDocs to provide better implementation guidance for non-standard cryptographic protocols. ZKDocs provides high-level summaries, protocol diagrams, important security considerations, and more for common non-standardized cryptographic protocols, like zero-knowledge proofs.

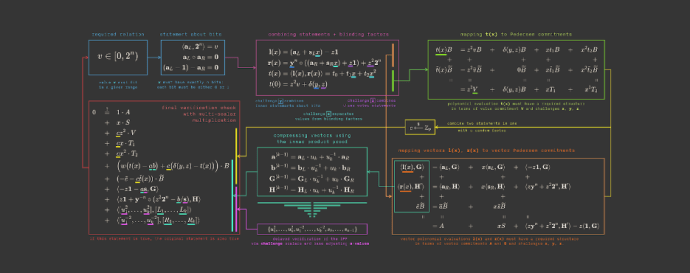
The inner product argument (IPA)

If you follow the cryptographic world, you may have heard of Bulletproofs, a type of zero-knowledge proof that has become popular in recent years. Despite their popularity, few people actually understand how these proofs actually work in detail because they are quite complicated! To get a sense for their complexity, check out this excellent protocol diagram from the dalek cryptography Bulletproofs implementation:

Bulletproofs protocol diagram (source)

The fundamental building block of Bulletproofs is the IPA. Like most cryptographic protocols, the IPA and Bulletproofs are so complex because they have been iteratively improved and refined over many years by theorists. The finished protocol is difficult to understand without the prior context of previous, simpler iterations. Fortunately, our new section in ZKDocs breaks down the IPA into simpler constructions and shows how these improvements can be made to achieve the final protocol being used today. Like all of ZKDocs, this section contains helpful protocol diagrams and important security considerations.

Commitment schemes

The concept of cryptographic commitment schemes is relatively intuitive: one person, the committer, first produces a cryptographic commitment that hides some secret value from all other observers, and then at a later time opens the commitment to reveal this value. For secure schemes, the commitment does not leak any information about the secret, and it’s impossible for the committer to equivocate on what this secret value was. The traditional commitment scheme allows the committer to commit to and reveal a specific value, usually an integer modulo a prime number.

Polynomial commitments are a generalization of scalar commitment schemes and an important building block in zero-knowledge protocols. Polynomial commitment schemes (PCSs) allow one party to prove to another the correct evaluation of a polynomial at some set of points, without revealing any other information about the polynomial.

We’ve updated ZKDocs with an explanation of the most common commitment scheme, Pedersen commitments, as well as of two common PCSs: the IPA PCS (derived from the IPA) and the KZG PCS.

Wide modular reduction

Many aspects of cryptography often deal with random values and prime numbers; a common requirement for various protocols is needing to generate a random value between 0 and p for some prime p. While this may sound relatively straightforward, in practice it is tricky to do securely.

The problem is that computers deal with bits and bytes. Typically, random number generators will produce a random number between 0 and 2n, where n is the number of requested random bits. Unfortunately, 2n is not a prime number and therefore cannot be directly used to generate a value between 0 and p for some p. This fundamental mismatch causes many people to generate their random numbers using the following obvious, simple, and INSECURE METHOD, which we detail in ZKDocs:

Insecure random sampling mod p (source)

ZKDocs documents a few different techniques to avoid the modulo bias described in the figure above. The nicest technique is known as wide modular reduction, and the concept is simple: if you have a prime p that has k bits, then generate a (k + 256)-bit random value (where 256 is a security parameter that can be tuned) and then reduce it mod p. (Note that this will also work with composite moduli, so p does not even have to be prime, but we use a prime since it is a common example). If you’re curious why this method is secure, the newest addition to ZKDocs breaks down the statistical argument as to why that’s the case.

We need your help!

We want to actively maintain and grow the content of ZKDocs. To make ZKDocs as effective as possible, we want to ensure that new content is helpful to the community. If you enjoy ZKDocs, please let us know what other content you’d like us to add! The best way to let us know is by raising an issue directly on the ZKDocs GitHub page.