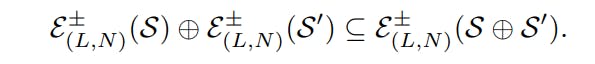
2024-6-9 21:30:22 Author: hackernoon.com(查看原文) 阅读量:2 收藏
Authors:
(1) Wahei Hara;
(2) Yuki Hirano.
Table of Links
- Abstract and Intro
- Exchanges and Mutations of modifying modules
- Quasi-symmetric representation and GIT quotient
- Main results
- Applications to Calabi-Yau complete intersections
- Appendix A. Matrix factorizations
- Appendix B. List of Notation
- References
2. Exchanges and Mutations of modifying modules
2.1. Noncommutative crepant resolution. The present section recalls the definition of some basic notions that are studied in this article.

(1) A reflexive R-module M is called a modifying module if EndR(M) is a (maximal) Cohen-Macaulay R-module.
(2) We say that a reflexive module M gives a noncommutative crepant resolution (=NCCR) Λ = EndR(M) if M is modifying and the algebra Λ has finite global dimension.
Remark 2.4. Note that our definition of NCCR is different from the one in [Van3] or [IW1]. However, if R is d-sCY, our definition is equivalent to other definitions. See [Van3, Lemma 4.2] or [IW1, Lemma 2.23].

from K ∈ addL such that the induced morphism α ◦ (−): Hom(N, K) → Hom(N, M) is surjective. If L = N, we just call α a right (addL)-approximation of M. A right (add L)N - approximation α: K → M of M is said to be minimal if any endomorphism φ ∈ End(K) satisfying α◦φ = α is an automorphism, and we say that α is reduced if any direct summand K′ of K does not contained in Ker(α). Note that if a right approximation is minimal, it is reduced, and in the case when R is complete local, the converse also holds.

Definition 2.6. Let R be a normal d-sCY, and let M, N, L ∈ ref R.

Lemma 2.7. Notation is same as above
(1) If L ′ ∈ addL, there is an inclusion

which remains to be true when restricting to reduced exchanges.
(2) If N′ ∈ add N, there is an inclusion

which remains to be true when restricting to reduced exchanges.
(3) For another full subcategory S ′ ⊆ ref R, there is an inclusion

If R is complete local, the similar inclusion also holds for reduced exchanges.
Proof. (1), (2) and the first assertion in (3) are obvious. The second assertion in (3) follows from the fact that, if R is complete local, two approximations α: K → M and α ′ : K′ → M′ are reduced if and only if α ⊕ α ′ : K ⊕ K′ → M ⊕ M′ is reduced.

Proof. Assume that Hom(N, M ⊕ N) is Cohen-Macaulay, and consider an exact sequence


0 → F Ker α → FK → FM → 0.
Now applying the functor Hom(−, FR) to this sequence together with the reflexive equivalence proves that the dual sequence
0 → M∗ → K∗ → (Ker α)
is exact.

0 → Hom(FM, FN) → Hom(FK, FN) → Hom(F Ker α, FN) → 0
remains to be exact. Since all modules in the original sequence are reflexive, the reflexive equivalence and the duality yield an isomorphism

and similar isomorphisms for K and Ker α, which imply the exactness of the sequence
0 → Hom(N ∗ , M∗ ) → Hom(N ∗ , K∗ ) → Hom(N ∗ ,(Ker α) ∗ ) → 0.
Thus the dual morphism
K∗ → (Ker α) ∗
is a right (add L ∗ )N∗ -approximation with the kernel M∗ , which proves the first assertion. The second assertion follows from a similar argument.
The following says that exchanging a direct summand of a modifying module gives a new modifying module in nice situations.

Lemma 2.10. Let M ∈ ref R. The following equivalence holds.
M ∈ CM R ⇐⇒ M∗ ∈ CM R
Proof. We may assume that R is local. Since M is reflexive, it is enough to show the direction (⇒). Since R is Gorenstein, its injective dimension is finite. Thus the result follows from [BH, Proposition 3.3.3 (b)].
Lemma 2.11. Let R be a Gorenstein normal ring, and let M, N ∈ ref R. Then

Proof. It is enough to prove the direction (⇒). Assume that Hom(M, N) ∈ CM R. Then Lemma 2.10 implies that Hom(M, N) ∗ ∈ CM R. But by Lemma [IW1, Lemma 2.9], there is an isomorphism Hom(M, N) ∗ ∼= Hom(N, M), which shows that Hom(N, M) ∈ CM R.

The proof for the case when m < 0 is similar.

Remark 2.13. Since a right approximation is not unique in general, neither is right/left mutation. However, right/left mutation is unique up to additive closure [IW1, Lemma 6.2], and if R is complete local, minimal mutations are unique up to isomorphism.

Theorem 2.14 ([IW1, Proposition 6.5, Theorem 6.8, Theorem 6.10]). Let M ∈ ref R be a modifying R-module.
2.3. Tilting bundles and mutations. This section discusses tilting bundles over algebraic stacks. We start from recalling some basic facts on the derived categories of algebraic stacks.




如有侵权请联系:admin#unsafe.sh