Table of Links

Abstract Introduction & Related Work

Method

Analysis & Results

Discussion & Conclusion

References

III. ANALYSIS & RESULTS

The research questions were investigated via a series of mediation analyses. Mediation analysis informs the relation between two variables by explaining how they are related [21]. The analysis models how a mediator variable transmits the effect of an independent variable X on a dependent variable Y. Path analysis is an extension of multiple regression that can examine chains of influence as well as several dependent variables [22]. The PROCESS macro for R (version 4.0.2) was used for all mediation analyses [23]. Mediation models tested the relationship between first impressions, trustworthiness, trust and intention to use. First impressions were split into its components warmth and competence and as these are thought to occur first, entered in turn as independent variable X for each model. Mediators were explored to predict the outcomes trust and intention use. A final model integrated all four concepts of interest in a serial parallel mediation.

A. Simple Mediation

The effect of warmth on trust was fully mediated via trustworthiness (see Fig. 2). The regression coefficient between warmth and trustworthiness as well as the regression coefficient between trustworthiness and trust were significant. The indirect effect was (.55) * (.73) = .40. The significance of the indirect effect was tested using 5,000 bootstrap samples and the 95% confidence interval ranged from 0.311 to 0.500. This means that 2.5% of the 5,000 bootstrap estimates were smaller than 0.311 and 2.5% were larger than 0.500. As this confidence interval does not include zero, we can reject the null hypothesis that T aT b = 0 and conclude that the indirect effect is statistically significant. There was a significant total effect (c = 0.48, 95% CI 0.385 to 0.581), but no significant direct effect (c ′ = 0.08, 95% CI -0.005 to 0.165).

Similarly, results showed that competence has a significant total effect on trust (c = 0.47, p < 0.001). Analyzing the indirect effects reveals that trustworthiness significantly mediates the relationship between competence and trust, ab = 0.45, p < 0.01 (95% CI 0.352 to 0.554). Competence positively affects trustworthiness (a = 0.59, p < 0.001) and trustworthiness, in turn, positively affects trust (b = 0.77, p < 0.001). After accounting for the mediating role of trustworthiness, the direct effect is not significant, indicating that the total effect is fully explained by the mediator (complete mediation). These findings provide some evidence that people who perceive a social robot as competent are more likely to trust it as they tend to also perceive its characteristics as trustworthy. However, people’s ratings of competence do not contribute to trust beyond what is accounted for by trustworthiness.

B. Parallel Mediation

Two parallel mediator models were designed to test the impact of the mediator trustworthiness in more detail. As trustworthiness is an index made up of the three subscales ability, benevolence and integrity, these constructs were next entered as parallel mediators. The indirect effect of warmth on trust through ability (X → M1 → Y), estimated as a1 ∗ b1 = 0.16 was significant (95% CI 0.089 to 0.241), as was the indirect effect of warmth on trust through benevolence (X → M2 → Y) estimated as a2 ∗ b2 = 0.13 (95% CI 0.049 to 0.239). However, integrity (X → M3 → Y) did not significantly mediate the relationship between warmth and trust (a3b3 = 0.10, 95% CI -0.002 to 0.218). Both the total effect (c = 0.48) and the direct effect (c ′ = 0.09) were statistically significant. A similar parallel mediator model, with the first impression of robot competence as independent variable instead of its warmth, confirmed this trend (see Fig. 3).

The indirect effect of competence on trust through ability (X → M1 → Y), estimated as a1 ∗ b1 = 0.18 was significant (95% CI 0.104 to 0.254), as was the indirect effect of competence on trust through benevolence (X → M2 → Y) estimated as a2 ∗ b2 = 0.14 (95% CI 0 0.053 to 0.248). However, even though the estimates for the individual legs a3 and b3 were significant (see Fig. 3), integrity (X → M3 → Y) did not significantly mediate the relationship between competence and trust as the confidence interval included zero (a3b3 = 0.12, 95% CI -0.007 to 0.248). The total effect (c = 0.47) was significant, however, the direct effect (c ′ = 0.03) was not. As integrity did not mediate the relationship between first impressions and trust when entered in parallel with ability and benevolence, a serial model will explore whether integrity in serial with ability and benevolence will provide a significant indirect effect as there is literature indicating this possibility [7].

C. Serial Parallel Mediation

Extending the previous two parallel mediator models, a serial model with integrity predicting ability and benevolence predicting trust was run. The direct effect of X on Y was fixed to zero. The indirect effect of warmth on trust through integrity and ability (X → M1 → M2 → Y), estimated as a1 ∗d21 ∗b2 = 0.59∗0.54∗0.50 = 0.16 was significant (95% CI 0.095 to 0.230). The indirect effect of warmth on trust through integrity and benevolence (X → M1 → M3 → Y), estimated as a1 ∗ d31 ∗ b3 = 0.59 ∗ 0.80 ∗ 0.39 = 0.18 was significant (see Fig. 4). The contrast was not significant.

A similar model with competence as the independent variable showed comparable results. The indirect effect of competence on trust through integrity and ability (a1 ∗ d21 ∗ b2 = 0.17) as well as the indirect effect through integrity and benevolence (a1 ∗ d31 ∗ b3 = 0.19) were significant.

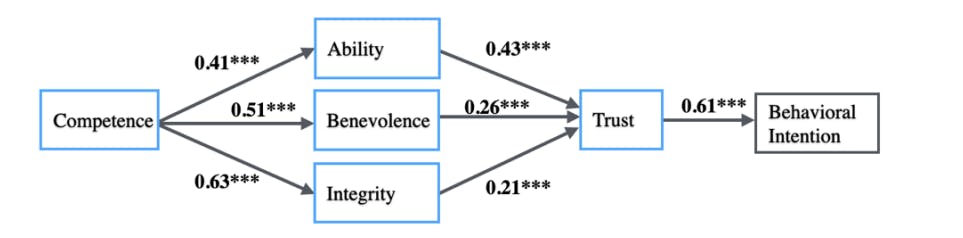
Finally, in order to express the relationship between first impressions, trustworthiness, trust and behavioral intention in one comprehensive model, a serial parallel mediation model was devised using PROCESS model 80 via B matrix specification. The direct effect of X on Y was fixed to zero. The indirect effect of competence on behavioral intention through ability and trust (X → M1 → M4 → Y), estimated as a1 ∗ d41 ∗ b4∗ = 0.41 ∗ 0.43 ∗ 0.61 = 0.11 was significant (95% CI 0.060 to 0.171).

Similarly, the indirect effects of competence on behavioral intention through benevolence and trust (X → M2 → M4 → Y), estimated as a2 ∗ d42 ∗ b4 = 0.08 and competence on behavioral intention through integrity and trust (X → M3 → M4 → Y), estimated as a ∗ d43 ∗ b4∗ = 0.08 were significant (see Fig. 5). A serial model with the first impression warmth as independent variable provided similar results. All indirect effects were significant (a1 ∗ d41 ∗ b4 = 0.10, a2 ∗ d42 ∗ b4 = 0.08, a3 ∗ d43 ∗ b4 = 0.08).