2024-10-21 09:21:42 Author: hackernoon.com(查看原文) 阅读量:0 收藏
Authors:
(1) Junwei Su, Department of Computer Science, the University of Hong Kong and [email protected];
(2) Chuan Wu, Department of Computer Science, the University of Hong Kong and [email protected].
Table of Links
5 A Case Study on Shortest-Path Distance
6 Conclusion and Discussion, and References
9 Procedure for Solving Eq. (6)
10 Additional Experiments Details and Results
11 Other Potential Applications
4 Main Results
In this section, we present the main results derived from our proposed framework for studying the generalization and fairness of GNNs with respect to different structural groups in a graph. We start by demonstrating the relationship between the generalization performance of the model and the structural distance between the subgroups and the training set (Theorem 1). We then show that such a structural relation can induce disparities in the generalization performance across different subgroups (Theorem 2). Finally, we connect these theoretical results to the recent deep learning spline line theory [2] to provide additional insights. Detailed proof of the results presented in this paper can be found in the supplementary material.
4.1 Generalization Performance and Structural Distance

Theorem 1 states that the generalization risk of a classifier with respect to a structural subgroup depends on the empirical training loss of the classifier, the structural distance between the subgroup and the training set, and the distortion (topology awareness) of GNNs. Such a relation provides a new perspective on understanding the link between topology awareness and generalization performance in GNNs. Prior research in this area has mainly focused on the connection between GNNs and the Weisfeiler-Lehman algorithm, emphasizing the ability of GNNs to differentiate various graph structures. However, Theorem 1 highlights a direct link between topology awareness and generalization performance, and a potential issue of fairness in GNNs, as it shows that the model’s performance on different structural subgroups is influenced by their distance to the training set. Next, we extend the result of Theorem 1 to analyze the relation between the generalization of different structural subgroups and their distance to the training set.
4.2 Unfair Generalization Performance on Structural Subgroups

Theorem 2 states that when comparing two subgroups, if the difference in their structural distance to the training set is larger than the threshold (δα), then GNNs exhibit unfair generalization performance with respect to these groups. Specifically, the theorem states that GNNs generalize better on subgroups that are structurally closer to the training set, which leads to accuracy disparities among different subgroups. Additionally, the theorem notes that the topology awareness of GNNs (measured by the distortion rate α) plays a key role in determining the strength of this accuracy disparity. This has important implications for the use of GNNs in critical applications, as it suggests that increased topology awareness in GNNs can lead to improved generalization performance but also a greater potential for unfairness in terms of accuracy disparities among different structural subgroups. As such, it is important to carefully consider the trade-offs between topology awareness and fairness when designing new GNNs and applying them to real-world problems.
4.3 Connection with Deep Learning Spline Theory
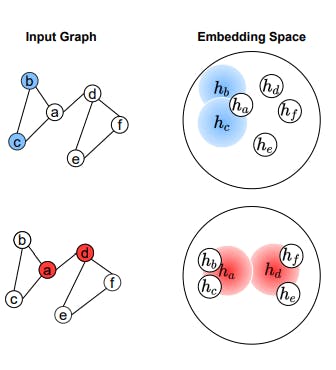
Our theoretical findings reveal that when considering the performance of the model from the viewpoint of the embedding space, the training set creates a “valley” effect on generalization performance, with the training vertex at the bottom of the valley. Representations that are closer to the embedding of the training set perform better, while those farther away perform worse. This pattern has an interesting connection with deep learning spline theory [2]. This theory suggests that in DNNs, the learning process for classification divides the input/latent space into small circles (referred to as power diagrams), where representations within each circle are grouped, and representations closer to the centre of the circle are predicted with more confidence. Our findings suggest that in GNNs, the mapping of test data to these power diagrams is related to the structural similarity between test and training data in the graph. This connection provides further validation for our derived results.

如有侵权请联系:admin#unsafe.sh