Table of Links

1. Abstract and Introduction
2. Related Work
3. Problem Definition
4. Method
5. Experiments
6. Conclusion and References

A. Appendix

A.1. Full Prompts and A.2 ICPL Details

A. 3 Baseline Details

A.4 Environment Details

A.5 Proxy Human Preference

A.6 Human-in-the-Loop Preference

5 EXPERIMENTS

In this section, we conducted two sets of experiments to evaluate the effectiveness of our method: one using proxy human preferences and the other using real human preferences.

1. Proxy Human Preference: In this experiment, human-designed rewards, taken from EUREKA (Ma et al., 2023), were used as proxies of human preferences. Specifically, if ground truth reward R1 > R2, sample 1 is preferred over sample 2. This method enables rapid and quantitative evaluation of our approach. It corresponds to a noise-free case that is likely easier than human trials; if ICPL performed poorly here it would be unlikely to work in human trials. Importantly, human-designed rewards were only used to automate the selection of samples and were not included in the prompts sent to the LLM; the LLM never observes the functional form of the ground truth rewards nor does it ever receive any values from them. Since proxy human preferences are free from noise, they offer a reliable comparison to evaluate our approach efficiently. However, as discussed later in the limitations section, these proxies may not correctly measure challenges in human feedback such as inability to rank samples, intransitive preferences, or other biases.

2) Human-in-the-loop Preference: To further validate our method, we conducted a second set of experiments with human participants. These participants repeated the tasks from the Proxy Human Preferences and engaged in an additional task that lacked a clear reward function: “Making a humanoid jump like a real human.”

5.1 TESTBED

All experiments were conducted on tasks from the Eureka benchmark (Ma et al., 2023) based on IsaacGym, covering a diverse range of environments: Cartpole, BallBalance, Quadcopter, Anymal, Humanoid, Ant, FrankaCabinet, ShadowHand, and AllegroHand. We adhered strictly to the original task configurations, including observation space, action space, and reward computation. This ensures that our method’s performance was evaluated under consistent and well-established conditions across a variety of domains.

5.2 BASELINES

We compared our method against two baselines:

Eureka (Ma et al., 2023). Eureka is an LLM-powered reward design method that uses sparse rewards as fitness scores. It consists of three main components: (1) zero-shot reward generation based on the environment context, (2) an evolutionary search that iteratively refines candidate reward functions, and (3) reward reflection, which allows further fine-tuning of the reward functions. Sparse rewards are used to select the best candidate reward function, which is then refined by the LLMs and incorporated as the “task score” in the reward reflection. In each iteration, Eureka generates 16 reward functions without checking their executability, assuming at least one will typically work across all considered environments in the first iteration. To ensure a fair comparison, we modified Eureka to generate a fixed number of executable reward functions, specifically K = 6 per iteration, the same as ICPL. This adjustment improves Eureka’s performance in more challenging tasks, where it often generates fewer executable reward functions.

PrefPPO (Lee et al.): B-Pref is a benchmark specifically designed for preference-based reinforcement learning. We use PrefPPO, one of the benchmark algorithms from B-Pref, as our preferencebased RL baseline. PrefPPO operates in a two-step process: first, the policy interacts with the environment, gathering experience and updating through the on-policy RL algorithm PPO to maximize the learned rewards. Then, the reward model is optimized via supervised learning based on feedback from a human teacher, with these steps repeated iteratively. To enhance performance, we incorporate unsupervised pretraining using intrinsic motivation at the beginning, which helps the agent explore the environment and collect diverse experiences. PrefPPO uses dense rewards as the preference metric for the simulated teacher, providing a more stronger and informative signal for labeling preferences. We adopt the original shaped reward functions from the IsaacGym tasks, which were developed by active reinforcement learning researchers who designed the tasks. Note that we also experimented with sparse rewards in PrefPPO and observed similar performance. Additionally, while the original PrefPPO provides feedback on fixed-length trajectory segments, we offer feedback on full trajectories of varying lengths to ensure a fair comparison with the preference acquisition method used in ICPL (i.e. having humans pick between full videos). Once the maximum number of human queries is reached, the reward model stops updating, and only the policy is updated using PPO. For more details, refer to Appendix A.3.

5.3 EXPERIMENT SETUP

5.3.1 TRAINING DETAILS

We use PPO as the reinforcement learning algorithm for all methods. For each task, we use the default hyperparameters of PPO provided by IsaacGym as these have previously been tuned to achieve high performance and were also used in our baselines, making a fairer comparison. We trained policies and rendered videos on a single A100 GPU machine. The total time for a full experiment was less than one day of wall clock time. We utilized GPT-4, specifically GPT-4-0613, as the backbone LLM for both our method, ICPL, and Eureka in the Proxy Human Preference experiment. For the Human-in-the-loop Preference experiment, we employ GPT-4o.

5.3.2 EVALUATION METRIC

Here, we provide a specific explanation of how sparse rewards (detailed in Appendix A.4) are used as task metrics in the adopted IsaacGym tasks. The task metric is the average of the sparse rewards across all environment instances. To assess the generated reward function or the learned reward model, we take the maximum task metric value from 10 policy checkpoints sampled at fixed intervals, marked as the task score of reward function/model denoted as (RTS).

Eureka can access the ground-truth task score and select the highest RTS from these iterations as the task score, denoted as (TS) for each experiment. For a fair comparison, ICPL also performs 5 iterations, selecting the highest RTS from these iterations as TS for each experiment. Unlike (Ma et al., 2023), which additionally conducts 5 independent PPO training runs for the reward function with the highest RTS and reports the average of 5 maximum task metric values from 10 policy checkpoints sampled at fixed intervals as the task score, we focus on selecting the best reward function according to human preferences, yielding policies better aligned with the task description. Due to the inherent randomness of LLM sampling, we run 5 experiments for all methods, including PrefPPO and EUREKA and report the highest TS as the final task score, denoted as (FTS), for each approach. A higher FTS indicates better performance across all tasks.

5.4 RESULTS OF PROXY HUMAN PREFERENCE

5.4.1 MAIN RESULTS

In ICPL, we use human-designed rewards as proxies to simulate ideal human preferences. Specifically, in each iteration, we select the reward function with the highest RTS as the good example and the reward function with the lowest RTS as the bad example for feedback. In Eureka, the reward function with the highest RTS is selected as the candidate reward function for feedback in each iteration. In PrefPPO, human-designed dense rewards are used as the preference metric: if the cumulative dense reward of trajectory 1 is greater than that of trajectory 2, then trajectory 1 is preferred over trajectory 2. Table 1 shows the final task score (FTS) for all methods across IsaacGym tasks.

For ICPL and PrefPPO, we track the number of synthetic queries Q required as a proxy for measuring the likely real human effort involved, which is crucial for methods that rely on human-in-the-loop preference feedback. Specifically, we define a single query as a human comparing two trajectories and providing a preference. In ICPL, each iteration generates K reward function samples, resulting in K corresponding videos. The human compares these videos, first selecting the best one, then picking the worst from the remaining K − 1 videos. After N = 5 iterations, the best video of each iteration is compared to select the overall best. The number of human queries Q can be calculated as Q = (K − 1) × 2N − 1. For ICPL, with K = 6 and N = 5, this results in Q = 49. In PrefPPO, the simulated human teacher compares two sampled trajectories and provides a preference label to update the reward model. We set the maximum number of queries to Q = 49, matching ICPL, and also test Q = 150, 1.5k, and 15k, denoted as PrefPPO-#Q in Table 1, to compare the final task score (FTS) across different tasks.

As shown in Table 1, for the simpler tasks like Cartpole and BallBalance, all methods achieve equal performance. Notably, we observe that for these particularly simple tasks, LLM-powered methods like Eureka and ICPL can generate correct reward functions in a zero-shot manner, without requiring feedback. As a result, ICPL only requires querying the human 5 times, while PrefPPO, after 5 queries, fails to train a reasonable reward model with the preference-labeled data. For relatively more challenging tasks, PrefPPO-49 performs significantly worse than ICPL when using the same

number of human queries. In fact, PrefPPO-49 fails in most tasks. As the number of human queries increases, PrefPPO’s performance improves across most tasks, but it still falls noticeably short compared to ICPL. This demonstrates that ICPL, with the integration of LLMs, can reduce human effort in preference-based learning by at least 30 times. Compared to Eureka, which uses task scores as a reward reflection signal, ICPL achieves comparable performance. This indicates that ICPL’s use of LLMs for preference learning is effective.

From the analysis conducted across 7 tasks where zero-shot generation of optimal reward functions was not feasible in the first iteration, we examined which iteration’s RTS was chosen as the final FTS. The distribution of RTS selections over iterations is illustrated in Fig. 2. The results indicate that FTS selections do not always come from the last iteration; some are also derived from earlier iterations. However, the majority of FTS selections originate from iterations 4 and 5, suggesting that ICPL is progressively refining and enhancing the reward functions over successive iterations as opposed to randomly generating diverse reward functions.

5.5 METHOD ANALYSIS

To validate the effectiveness of ICPL’s module design, we conducted ablation studies. We aim to answer several questions that could undermine the results presented here:

1. Are components such as the reward trace or the reward difference helpful?

2. Is the LLM actually performing preference learning? Or is it simply zero-shot outputting the correct reward function due to the task being in the training data?

5.5.1 ABLATIONS

The results of the ablations are shown in Table 2. In these studies, “ICPL w/o RT” refers to removing the reward trace from the prompts sent to the LLMs. “ICPL w/o RTD” indicates the removal of both the reward trace and the differences between historical reward functions from the prompts. “ICPL w/o RTDB” removes the reward trace, differences between historical reward functions, and bad reward functions, leaving only the good reward functions and their evaluation in the prompts. The “OpenLoop” configuration samples K × N reward functions without any feedback, corresponding to the ability of the LLM to zero-shot accomplish the task.

Due to the large variance of the experiments (see Appendix), we mark the top two results in bold. As shown, ICPL achieves top 2 results in 8 out of 9 tasks and is comparable on the Allegro task. The “OpenLoop” configuration performs the worst, indicating that our method does not solely rely on GPT-4’s either having randomly produced the right reward function or having memorized the reward function during its training. This improvement is further demonstrated in Sec. 5.5.2, where we show the step-by-step improvements of ICPL through proxy human preference feedback. Additionally, “ICPL w/o RT” underperforms on multiple tasks, highlighting the importance of incorporating the reward trace of historical reward functions into the prompts.

5.5.2 IMPROVEMENT ANALYSIS

Table 1 presents the performance achieved by ICPL. While it is possible that the LLMs could generate an optimal reward function in a zero-shot manner, the primary focus of our analysis is not solely on absolute performance values. Rather, we emphasize whether ICPL is capable of enhancing performance through the iterative incorporation of preferences. We calculated the average RTS

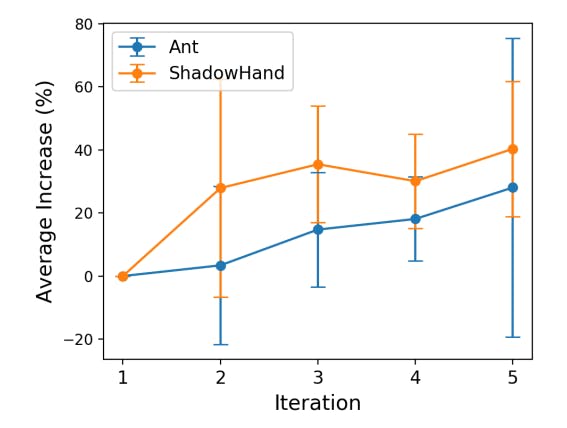
improvement over iterations relative to the first iteration for the two tasks with the largest improvements compared with “OpenLoop”, Ant and ShadowHand. As shown in Fig. 3, the RTS exhibits an upward trend, demonstrating its effectiveness in improving reward functions over time. We note that this trend is roughly monotonic, indicating that on average the LLM is using the preferences to construct reward functions that are closer to the ground-truth reward. We further use an example in the Humanoid task to demonstrate how ICPL progressively generated improved reward functions over successive iterations in Appendix A.5.2.

5.6 RESULTS OF HUMAN-IN-THE-LOOP PREFERENCE

To address the limitations of proxy human preferences, which simulate idealized human preference and may not fully capture the challenges humans may face in providing preferences, we conducted experiments with real human participants. We recruited 6 volunteers to participate in human-inthe-loop experiments, including 5 tasks from IsaacGym and a newly designed task. None of the volunteers had prior experience with these tasks, ensuring an unbiased evaluation based on their preferences.

5.6.1 HUMAN EXPERIMENT SETUP

Before the experiment, each volunteer was provided with a detailed explanation of the experiment’s purpose and process. Additionally, volunteers were fully informed of their rights, and written consent was obtained from each participant. The experimental procedure was approved by the department’s ethics committee to ensure compliance with institutional guidelines on human subject research.

More specifically, each volunteer was assigned an account with a pre-configured environment to ensure smooth operation. After starting the experiment, LLMs generated the first iteration of reward functions. Once the reinforcement learning training was completed, videos corresponding to the policies derived from each reward function were automatically rendered. Volunteers compared the behaviors in the videos with the task descriptions and selected both the best and the worst-performing videos. They then entered the respective identifiers of these videos into the interactive interface and pressed “Enter” to proceed. The human preference was processed as an LLM prompt for generating feedback, leading to the next iteration of reward function generation.

This training-rendering-selection process was repeated across 4 iterations. At the end of the final iteration, the volunteers were asked to select the best video from those previously marked as good, designating it as the final result of the experiment. For IsaacGym tasks, the corresponding RTS was recorded as TS. It is important to note that, unlike proxy human preference experiments where the TS is the maximum RTS across iterations, in the human-in-the-loop preference experiment, TS

refers to the highest RTS chosen by the human, as human selections are not always based on the maximum RTS at each iteration. Given that ICPL required reinforcement learning training in every iteration, each experiment lasted two to three days. Each volunteer was assigned a specific task and conducted five experiments, one for each task, with the highest TS being recorded as FTS in IsaacGym tasks.

5.6.2 ISAACGYM TASKS

Due to the simplicity of the Cartpole, BallBalance, Franka tasks, where LLMs were able to zeroshot generate correct reward functions without any feedback, these tasks were excluded from the human trials. The Anymal task, which involved commanding a robotic dog to follow random commands, was also excluded as it was difficult for humans to evaluate whether the commands were followed based solely on the videos. For the 5 adopted tasks, we describe in the Appendix A.6.1 how humans infer tasks through videos and the potential reasons that may lead to preference rankings that do not accurately reflect the task.

Table 3 presents the FTS for the human-in-the-loop preference experiments conducted across 5 suitable IsaacGym tasks, labeled as “ICPL-real”. The results of the proxy human preference experiment are labeled as “ICPL-proxy”. As observed, the performance of “ICPL-real” is comparable or slightly lower than that of “ICPL-proxy” in all 5 tasks, yet it still outperforms the “OpenLoop” results in 3 out of 5 tasks. This indicates that while humans may have difficulty providing consistent preferences from videos as proxies, their feedback can still be effective in improving performance when combined with LLMs.

5.6.3 HUMANOIDJUMP TASK

In our study, we introduced a new task: HumanoidJump, with the task description being “to make humanoid jump like a real human.” Defining a precise task metric for this objective is challenging, as the criteria for human-like jumping are not easily quantifiable. The task-specific prompts used in this experiment are detailed in the Appendix A.6.2.

The most common behavior observed in this task, as illustrated in Fig. 4, is what we refer to as the “leg-lift jump.” This behavior involves initially lifting one leg to raise the center of mass, followed by the opposite leg pushing off the ground to achieve lift. The previously lifted leg is then lowered to extend airtime. Various adjustments of the center of mass with the lifted leg were also noted. This behavior meets the minimal metric of a jump: achieving a certain distance off the ground. If feedback were provided based solely on this minimal metric, the “leg-lift jump” would likely be selected as a candidate reward function. However, such candidates show limited improvement in subsequent iterations, failing to evolve into more human-like jumping behaviors.

Conversely, when real human preferences were used to guide the task, the results were notably different. The volunteer judged the overall quality of the humanoid’s jump behavior instead of just the metric of leaving the ground. Fig. 5 illustrates an example where the volunteer successfully guided the humanoid towards a more human-like jump by selecting behaviors that, while initially not optimal, displayed promising movement patterns. The reward functions are shown in Appendix A.6.2. In the first iteration, “leg-lift jump” was not selected despite the humanoid jumping off the ground. Instead, a video where the humanoid appears to attempt a jump using both legs, without leaving the ground, was chosen. By the fifth and sixth iterations, the humanoid demonstrated more

sophisticated behaviors, such as bending both legs and lowering the upper body to shift the center of mass, behaviors that are much more akin to a real human jump.