• 本文目的：写这篇文章的目的主要是整理下密码学中Base64的知识点，并把它们分享出来。并且帮助初探密码学的坛友们一步一步的用C语言将Base64的编码实现出来。
• 阅读方法：希望大家在浏览完本片文章后可以自己去实现一下，相信一定会对你的编程技术有所提高。(附件中提供参考代码)
• 具备基础：
  (1)熟练掌握C语言
• 学习环境：任意C语言开发环境, Base64加解密工具

　　虽然这篇文章发布在密码算法区，但希望大家不要误解，Base64并不是一种加密的方法，而是一种编码的方式。虽然用Base64加密(暂且说是加密)的字符串看起来有一种被加密的感觉，但是这只是感觉。因为如果用标准的Base64进行加密会发现很多Base64的特征，比如在Base64字符串中会出现'+'和'\'两种字符，在字符串的末尾经常会有一个到两个连续的'='。只要发现了这些特征，就可以肯定这个字符串被Base64加密过，只要通过相应的解密小程序就可以轻松得到加密前的样子(非标准的除外)。
　　那么有为什么说Base64是一中编码方式呢？这是因为Base64可以把所有的二进制数据都转换成ASCII码可打印字符串的形式。以便在只支持文本的环境中也能够顺利地传输二进制数据。当然有时在CTF的题目中掺杂上非标准的Base64编码表也会有加密的效果，但是如果找到这个表那就编程明文了，所以在CTF题目中只会起到辅助的作用。

　　Base64编码的核心原理是将二进制数据进行分组，每24Bit(3字节)为一个大组，再把一个大组的数据分成4个6Bit的小分组。由于6Bit数据只能表示64个不同的字符(2^6=64)，所以这也是Base64的名字由来。这64个字符分别对应ASCII码表中的'A'-'Z'，'a'-'z'，'0''9'，'+'和'/'。他们的对应关系是由Base64字符集决定的。因为小分组中的6Bit数据表示起来并不方便，所以要把每个小分组进行高位补零操作，这样每个小分组就构成了一个8Bit(字节)的数据。在补零操作完成后接下来的工作就简单多了，那就是将小分组的内容作为Base64字符集的下标，然后一一替换成对应的ASCII字符。加密工作完成。

　　Base64解密的工作原理也非常的简单，只要操作方式和加密步骤相反即可。首先将Base64编码根据其对应的字符集转换成下标，这就是补完零后的8Bit(一字节)数据。既然有补零操作那自然会有去零操作了，我们要将这些8Bit数据的最高位上的两个0抹去形成6Bit数据，这也就是前面我们提到过的小分组。最后就是将每4个6Bit数据进行合并形成24Bit的大分组，然后将这些大分组按照每组8Bit进行拆分就会得到3个8Bit的数据，这写8Bit数据就是加密前的数据了。解密工作完成。

　　重点：别看前面说的Base64工作流程这么简单，实际上里面还是有很多坑的，那在我们了解了编码原理后现在就来填坑了：
　　我们在Base64编码前是无法保证准备编码的字符串长度是3的倍数，所以为了让编码能够顺利进行就必须在获取编码字符串的同时判断字符串的长度是否是3的倍数，如果是3的倍数编码就可以正常进行，如果不是那么就要进行额外的操作——补零，就是要在不足3的倍数的字符串末尾用0x00进行填充。
　　这样就是解决了字符串长度不足的问题了，但是同时也引进了另一个新的问题，那就是末尾补充上的0在进行Base64字符集替换的时候会与字符集中的'A'字符发生冲突。因为字符集中的下标0对应的字符是'A'，而末尾填充上的0x00在分组补零后同样是下标0x00，这样就无法分辨出到底是末尾填充的0x00还是二进制数据中的0x00。为了解决这个问题我们就必须引入Base64字符集外的新字符来区分末尾补充上的0x00，这就是'='字符不在Base64字符集中，但是也出现在Base64编码的原因了，'='字符在一个Base64编码的末尾中最多会出现两个，如果不符合这以规则那么这个Base64就可能被人做了手脚。

Base64字符集：

我们以输入字符串"6666"为例:　　

1、判断字符串长度，不足3的倍数用0x00填充:

2、将补零后的字符串进行8Bit分组:

3、把每个大分组进行6Bit分组：

4、将6Bit组转换成Base64字符集的下标:
(注:由于是进行图片解说，所以省区了6Bit组高位补零操作!)

5、把字符集的下标替换成Base64字符:

6、修正末尾的符号，得到Base64编码结果

解密操作和加密操作相反！

0x00 Base64加密部分:

1、将长度补全后的字符串转换成6Bit分组:

int TransitionSixBitGroup(unsigned char *BitPlainText, unsigned char* SixBitGroup, unsigned int SixBitGroupSize)
{
    int ret = 0;

    //1、每4个6Bit组一个循环
    for (int i = 0, j = 0; i < SixBitGroupSize; i += 4, j += 3)
    {
        SixBitGroup[i]        = ((BitPlainText[j] & 0xFC) >> 2);
        SixBitGroup[i + 1]    = ((BitPlainText[j] & 0x03) << 4) + ((BitPlainText[j + 1] & 0xF0) >> 4);
        SixBitGroup[i + 2]    = ((BitPlainText[j + 1] & 0x0F) << 2) + ((BitPlainText[j + 2] & 0xC0) >> 6);
        SixBitGroup[i + 3]    = (BitPlainText[j + 2] & 0x3F);
    }

    return ret;
}

　　这一段代码的功能是将已经补足长度的16进制数据转变成6Bit分组，每一个分组用8Bit(一个字节)表示，所以也就自动完成了6Bit组的高位补零操作。这里用到了一个for循环，其目的是为了达到前面所说的分组，这里分了两个部分，一部分是将16进制数据分成一个38Bit的大分组，另一部分是将大分组中的数据分割成46Bit的小分组，分割的过程用到了很多位操作，大大降低了分组的复杂性，只不过需要注意运算法的优先级。
　　语句剖析:
　　SixBitGroup[i] = ((BitPlainText[j] & 0xFC) >> 2); //在38Bit数据中的第一个数据取6Bit内容右移两位得到第一个6Bit数据。

　　SixBitGroup[i + 1] = ((BitPlainText[j] & 0x03) << 4) + ((BitPlainText[j + 1] & 0xF0) >> 4);//在38Bit数据中的第一个数据取2Bit内容后左移4位，加上38Bit数据中的第二个数据取4Bit数据构成第二个6Bit数据。

　　SixBitGroup[i + 2] = ((BitPlainText[j + 1] & 0x0F) << 2) + ((BitPlainText[j + 2] & 0xC0) >> 6);//在38Bit数据中的第二个数据取4Bit内容后左移2位，加上38Bit数据中的第三个数据取2Bit数据右移6位构成第三个6Bit数据。

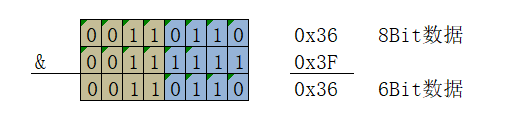
　　SixBitGroup[i + 3] = (BitPlainText[j + 2] & 0x3F);//在38Bit数据中的第三个数据取6Bit数据得到最后一个6Bit数据。

2、根据6Bit组获取字符串:

unsigned char Base64Table[64] =
{
    'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H',
    'I', 'G', 'K', 'L', 'M', 'N', 'O', 'P',
    'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X',
    'Y', 'Z', 'a', 'b', 'c', 'd', 'e', 'f',
    'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n',
    'o', 'p', 'q', 'r', 's', 't', 'u', 'v',
    'w', 'x', 'y', 'z', '0', '1', '2', '3',
    '4', '5', '6', '7', '8', '9', '+', '/'
};

int GetBase64String(unsigned char *CipherGroup, unsigned char *SixBitGroup, unsigned int SixBitGroupSize)
{
    int ret = 0;

    for (int i = 0; i < SixBitGroupSize; i++)
    {
        CipherGroup[i] = Base64Table[SixBitGroup[i]];
    }

    return ret;
}

　　通过第一步的处理，我们得到了Base64的高位补零后的6Bit分组也就是Base64字符集的下标。通过下标获取Base64字符集中的内容也就非常简单了，利用for循环进行查表赋值操作就可以初步得到Base64的编码值了。

3、将初步得到Base64的编码值末尾补充的字符转换成'=':

    for (int i = SixBitGroupSize - 1; i > SixBitGroupSize - 3; i--)
    {
        if (CipherGroup[i] == 'A')
        {
            CipherGroup[i] = '=';
        }
    }

　　因为Base64编码最多只可能出现两个'='字符，所以判断条件为i > SixBitGroupSize-3，并且在循环中判断末尾是否是补充字符。经过这一过程，也就获取了Base64加密后的结果。加密完成！

0x01 Base64解密部分:

1、将Base64密文转换成Base64下标：

int GetBase64Index(unsigned char *CipherText, unsigned char *Base64Index, unsigned int Base64IndexSize)
{
    int ret = 0;

    for (int i = 0; i < Base64IndexSize; i++)
    {
        //计算下标
        if (CipherText[i] >= 'A' && CipherText[i] <= 'Z')    //'A'-'Z'
        {
            Base64Index[i] = CipherText[i] - 'A';
        }
        else if (CipherText[i] >= 'a' && CipherText[i] <= 'z')    //'a'-'z'
        {
            Base64Index[i] = CipherText[i] - 'a' + 26;
        }
        else if (CipherText[i] >= '0' && CipherText[i] <= '9')    //'0'-'9'
        {
            Base64Index[i] = CipherText[i] - '0' + 52;
        }
        else if (CipherText[i] == '+')
        {
            Base64Index[i] = 62;
        }
        else if (CipherText[i] == '/')
        {
            Base64Index[i] = 63;
        }
        else    //处理字符串末尾是'='的情况
        {
            Base64Index[i] = 0;
        }
    }

    return ret;
}

　　由于Base64字符串是用ASCII码表示的，所以要想获取其对应的索引号就需要减去每一段ASCII第一个字符后加上相应的偏移，最后应该注意的是不要忘记还有一个不在Base64字符集的字符。

2、将Base64下标(6Bit组)转换为明文字符串的8Bit组形式

int TransitionEightBitGroup(unsigned char *BitPlainText, unsigned char *Base64Index, unsigned int Base64IndexSize)
{
    int ret = 0;

    for (int i = 0, j = 0; j < Base64IndexSize; i += 3, j += 4)
    {
        BitPlainText[i]        = (Base64Index[j] << 2) + ((Base64Index[j + 1] & 0xF0) >> 4);
        BitPlainText[i + 1]    = ((Base64Index[j + 1] & 0x0F) << 4) + ((Base64Index[j + 2] & 0xFC) >> 2);
        BitPlainText[i + 2]    = ((Base64Index[j + 2] & 0x03) << 6) + Base64Index[j + 3];
    }
F
    return ret;
}

　　这里进行的位操作有点不容易理解，但是它的作用就是把46Bit组中高位填充的0x00去掉后合并成38Bit的明文数据。需要留心下位操作的运算符优先级和处理的数据位。最后得到的结果就是16进制数据了。解密完成！
　　语句剖析:
　　BitPlainText[i] = (Base64Index[j] << 2) + ((Base64Index[j + 1] & 0xF0) >> 4);//将第一个46Bit组数据左移2位去除高位补的0x00得到6个有效Bit位，从第二个46Bit组取得4Bit数据右移4位(包含两个有效位)，两个部分相加得到第一个38Bit组数据。

　　BitPlainText[i + 1] = ((Base64Index[j + 1] & 0x0F) << 4) + ((Base64Index[j + 2] & 0x3C) >> 2);//从第二个46Bit组取得4Bit数据左移4位得到4个有效Bit位，从第三个46Bit组取得6Bit数据右移2位得到4个有效Bit位，两个部分相加得到第二个38Bit组数据。

　　BitPlainText[i + 2] = ((Base64Index[j + 2] & 0x03) << 6) + Base64Index[j + 3];//从第三个46Bit组取得2Bit数据左移6位得到2个有效Bit位，从第四个46Bit组取得8Bit数据得到6个有效Bit位，两个部分相加得到第三个3*8Bit组数据。

　　写到这里，我对Base64算法的理解也就分享完了。其实Base64的原理非常简单，但是实现它的过程却十分的有意思，它展现了C语言中位操作的魅力。我感觉只有对位操作有着深入的理解，才能更好的进行密码学的学习。

不知道是为什么在核心代码讲解部分，完全不知道要写些什么。。。。

[公告]看雪2019安全开发者峰会(SDC)满意度调查表！

最后于 5小时前 被QiuJYu编辑 ，原因：